Bakteriumwachstum - oder die biologische Ignoranz des Stefan Homburg

Am 03.02.2021 schrieb Querdenkerprofessor Stefan Homburg:

»Die Mathematikkenntnisse von Biologen sind ja notorisch. Wenn Sie die Tabelle lesen und versehen, [sic] dann merken Sie, dass ein Sigmoid keine "exponentielle" Phase hat (mit konstanter Wachstumsrate), sondern nur eine konvexe (mit zunehmender Steigung und abnehmender Wachstumsrate).«

Er bezieht sich dabei auf eine Grafik, in der als Beispiel für einen sigmoiden Verlauf eines Graphen u. A. Bakterienwachstum angegeben wurde und verkündet seine Überlegenheit in der Mathematik. Was er tatsächlich demonstriert, ist allerdings seine groteske Unterlegenheit in der Biologie. Das oben zitierte Bashing gegen Biologïnnen gibt er ab, als ein User ihn (korrekterweise) darauf hinweist, dass es beim Bakterienwachstum um eine exponentielle Phase innerhalb der sigmoidalen Kurve geht. Homburgs Antwort ist, dass alle Biologiebücher falsch sind, da sie exponentiell und konvex verwechseln würden.

Erst mal der Schocker: Nein, die Gesamtheit der Biologiebücher liegt natürlich nicht falsch. Zwar müssen nicht alle sigmoiden Kurven einen exponetiellen Teil enthalten, logistische Sigmoidkurven, die beim Bakterienwachstum eine Rolle spielen, haben allerdings einen solchen exponentiellen Abschnitt. Weil Stefan Homburg aber keine Ahnung von Biologie hat, meint er zu der von ihm gezeigten Grafik, die explizit Bakterienkulturen erwähnt, dass Biologïnnen sie fehlinterpretieren würden.

Der Mann versucht damit verzweifelt, dieses »Ich weiß es besser und deswegen ist die Pandemie nicht weiter schlimm!«-Narrativ zu erhalten.

Fakt ist aber, dass es im Bakterienwachstum eine Phase gibt, in der sich die Anzahl der Bakterien regelmäßig verdoppelt, weil es genügend Nährstoffe und Platz für alle gibt.

Man sollte meinen, das könne sofort mit dem ersten Bakterium beginnen, weil das ja auch genug Platz und Nährstoffe hat. Das ist real aber nicht so. Real muss sich ein Bakterium erst mal an ein neues Medium anpassen, bevor es sich so richtig effizient vermehren kann. Deshalb gibt es eine kurze Phase, in der das Wachstum noch etwas langsamer läuft. Hier wird mit Rezeptoren die Umgebung erfasst und die Proteinexpression auf die optimale Nährstoffnutzung in der Umgebung angepasst. Dann beginnt die Phase, in der jedes einzelne Bakterium super an das Nährstoffangebot angepasst ist, sich regelmäßig teilt und die jeweiligen Klone genauso gut angepasst sind. Die teilen sich dann wieder - und deren Klone teilen sich dann auch wieder. Da die Zeit nach einer Teilung bis zu nächsten Teilung ungefähr gleich ist, und sich jeder Klon genauso gut teilt, wie das Bakterium, aus dem er erstanden ist, kann man sich eigentlich logisch vorstellen, dass das Wachstum in diesem Moment exponentiell verläuft.
4k Bakterien teilen sich zu 8k, 8k zu 16k, 16k zu 32k und so weiter.

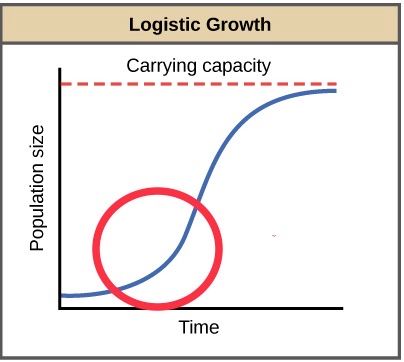
Würde man diesen Abschnitt der Kurve isoliert betrachten, würde man einfach nur eine exponentielle Kurve sehen. Den Mathematikerïnnen der Welt würde beim Betrachten nicht auffallen, dass dieser Abschnitt Teil einer sigmoiden Kurve sein müsste.

Das könnte jetzt ja ewig so weiter gehen, aber diese Beschreibung des Bakteriumwachstums bezieht sich auf eine ganz bestimmte Situation - nämlich auf das Wachstum von Zellen auf oder in einem Nährmedium.

Das bedeutet

1. Es gibt keine Fressfeinde
2. Es gibt keine Konkurrenz, außer die eigenen Klone
3. Es gibt keine Zufuhr von neuem Medium mit neuen Nährstoffen
4. Der Platz ist endlich

So. Und irgendwann ist dann da nichts mehr zu essen, bzw. es ist viel schwerer an etwas heran zu kommen - und schlimmstenfalls ist auch kein Platz mehr um sich weiter zu vermehren. Die exponentielle Phase muss damit einfach enden.

Wir sind jetzt in der stationären Phase. Es ist weniger Wachstum möglich, weil sich nur noch die Zellen teilen, die genügen Nährstoffe ergattern können. Es dauert auch länger, bis die Bakterien sich teilen, da sie erst mal genug Energie in Form von Nährstoffen sammeln müssen, die ja jetzt nicht mehr so leicht zu finden sind. Also:

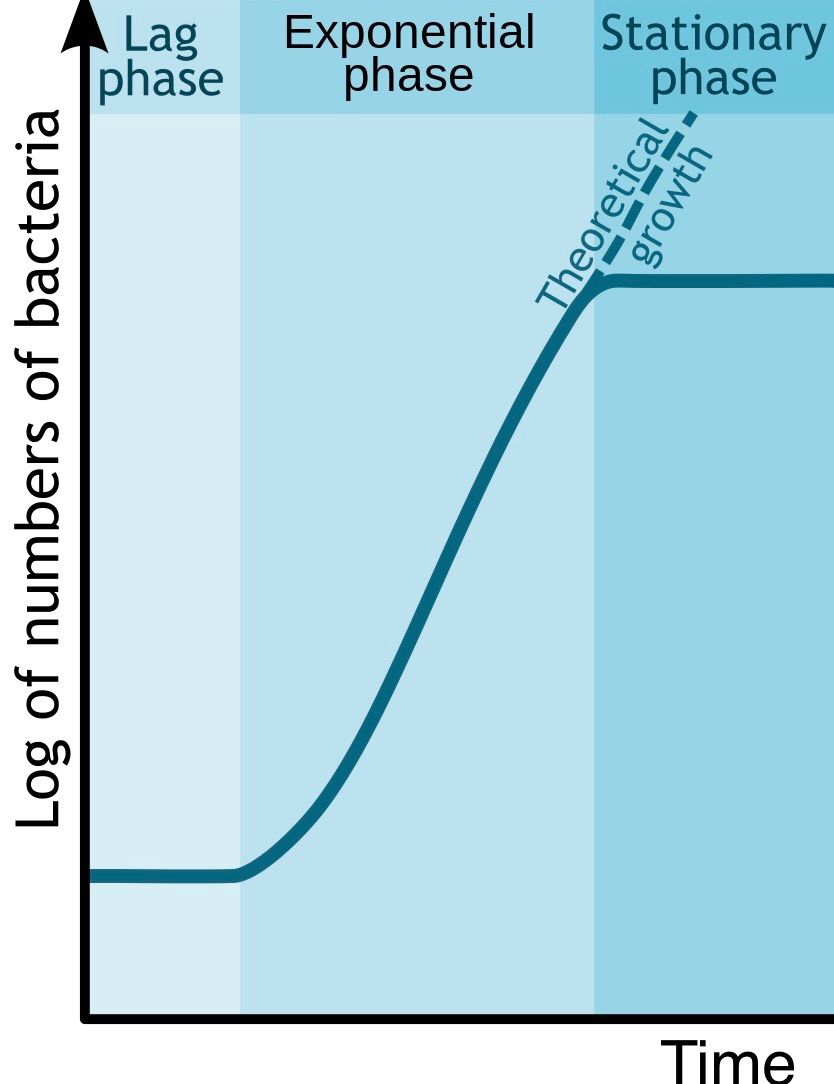
1. Phase ist die lag-Phase, also die Verzögerungsphase, in der sich das Bakterium anpasst, bevor es mit der Vermehrung so richtig loslegt.
2. Phase ist die log-Phase, da hier der Exponent der Phase mit einer logarithmischen Funktion beschrieben werden kann. Das ist übrigens etwas, das in der 10. Klasse gelehrt wird. Damit müsste also auch ein Prof. Homburg vertraut sein.
3. Phase ist die stationäre Phase. Ein unglücklicher Begriff, da die Kurve hier zwar abflacht, aber nicht langfristig auf nur einem Niveau bleibt.

Und wenn ihr jetzt noch mal richtig über Homburg lachen wollt: Das ist nicht das Ende der Beschreibung des Bakterienwachstums!

Es gibt eine 4. Phase: Denn was passiert denn, wenn fast alle Nährstoffe aufgebraucht sind? Bakterien brauchen die ja nicht nur zum Teilen, sondern auch zum Überleben. Und jetzt ist da dank exponentieller log-Phase eine ganze Masse an Bakos, und die hat Hunger!
Naja: 😵 Wer nicht hat, was er zum Überleben braucht, überlebt halt nicht.
Tatsächlich sieht das also so aus: Die Bakterien sterben nun nach und nach. Von den dadurch freigegebenen Nähestoffen und Überresten können andere Bakterien sich vielleicht noch ein bisschen ernähren, aber irgendwann ist eben nichts mehr da. Zudem entstehen dabei toxische Stoffe, die den noch lebenden Bakterien schaden*.

Die 4. Phase nennt sich die Absterbephase.

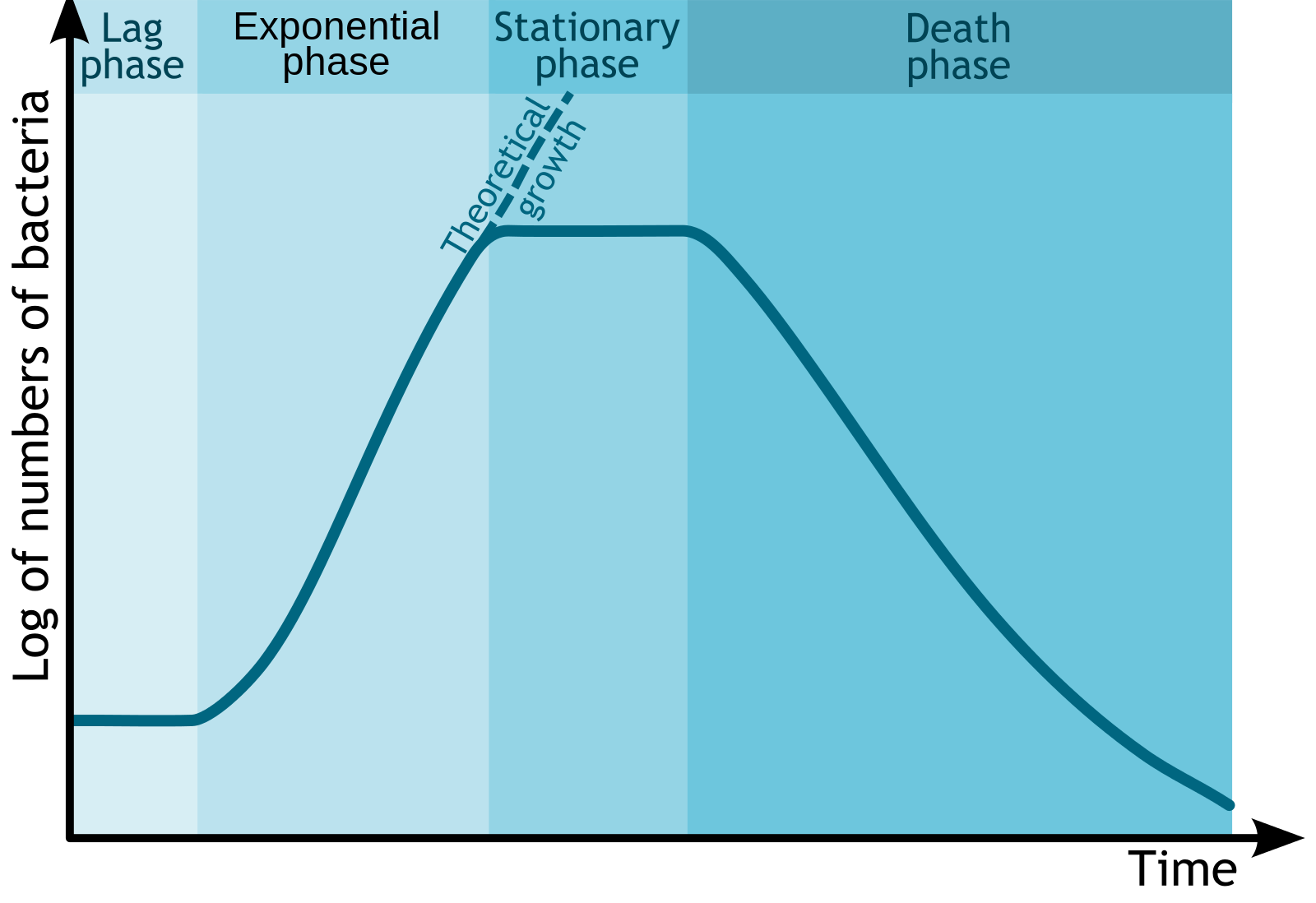
Damit ist die gesamte Kurve jetzt auch nicht mal mehr  näherungsweise sigmoidal. Nur ein Teil von ihr entspricht dieser Beschreibung - und ein Teil dieses Teils entspricht einer Exponentialkurve. Das ist halt die Ironie daran: Homburg hat sich einen Abschnitt des Bakteriumwachstums heraus gepickt, um zu behaupten, dass es nicht legitim ist, einen Abschnitt dieses Abschnitts separat zu beschreiben. Nochmal: Hätte er nur die exponentielle Phase des Bakteriumwachstums gesehen, er hätte mathematisch nicht feststellen können, dass diese Phase Teil einer sigmoiden Kurve ist!

So. Warum brauchen Biologïnnen den Scheiß eigentlich?

Bakterien sind Werkzeuge in der Biologie. Man kann ihnen Gene einpflanzen, um entweder diese Gene zu vermehren oder um das zu vermehren, was die Bakterien aufgrund dieser Gene produzieren. Da man möglichst effizient arbeiten will, versucht man Bakterien so lange wachsen zu lassen, dass man möglichst viel Material aus der Population aufreinigen kann, aber so früh wie möglich erntet - gegen Ende der exponentiellen Phase, wenn es die meisten Bakterien gibt, aber jede längere Inkubation zu einem langsameren Wachstum und sogar zu deren langsamen Absterben führen würde. Das wäre natürlich ineffizient.

Praktisch haben Labore für ihre Verfahren, Nährmedien und Bakterien natürlich ein Protokoll, bei dem sie bereits wissen, nach wie viel Inkubationszeit der beste Zeitpunkt für die Ernte ist.
Praktisch schaut man sich beim Ermitteln des Zeitpunkts die Trübung des Mediums mittels Photometer an (also die Verringerung der Lichtdurchlässigkeit), denn Bakterien trüben das Medium schon allein durch ihre Anwesenheit.

Das Wissen um die exponentielle Natur der Wachstumsphase ist für Biologïnnen nur Grundwissen, das sie für den richtigen Umgang mit ihren alltäglichen biologischen Werkzeugen benötigen. Für Homburg scheint seine persönliche Verwirrung darüber, dass sigmoide Kurven eine exponentielle Phase überhaupt nicht ausschließen, ein absolutes Phänomen zu sein. Er ist, sozusagen, über seine eigene Ignoranz gestolpert.

Kurz: Homburg rennt mal wieder in anderer Menschen Fachgebiete und versagt dabei katastrophal. Alles wie immer, würde ich sagen.

-DailyKaffee

* vielen Dank an Minnatriumazid (Twitter: @DieMinna) für die Ergänzung. Danke auch an Bissiges Mäuschen (@BMauschen) für die Inspiration zu dem Artikel.