Keine Sorge, wir brauchen dafür nur Abiwissen Mathe+Physik, versprochen! Der Beispielcode ist in Python geschrieben und mit allgemeinem Programmierwissen sollte man ihn problemlos nachvollziehen können.
Jedes Objekt im Sonnensystem hat drei Eigenschaften, die für uns relevant sind: Masse, Position und Geschwindigkeit. Wenn wir diese Werte kennen, dann können wir gemäß Newtons Schwerkraftgesetz die Kräfte und Beschleunigungen im System ausrechnen. Wir nehmen dann näherungsweise an, dass die Beschleunigungen für einen kurzen Zeitraum Δt konstant bleiben und berechnen, wie sich das System weiterentwickelt.
Wir werden dafür mit dreidimensionalen Vektoren rechnen müssen. Wenn wir eine Library dafür haben, ist das in Ordnung, ansonsten basteln wir uns schnell selber was.
class Vector:
def __init__(self, x, y, z):
self.x = x
self.y = y
self.z = z
def __add__(self, other):
x = self.x + other.x
y = self.y + other.y
z = self.z + other.z
return Vector(x, y, z)
def __sub__(self, other):
x = self.x - other.x
y = self.y - other.y
z = self.z - other.z
return Vector(x, y, z)
def __mul__(self, scalar):
x = self.x * scalar
y = self.y * scalar
z = self.z * scalar
return Vector(x, y, z)
def __rmul__(self, scalar):
return self * scalar
def __truediv__(self, scalar):
x = self.x / scalar
y = self.y / scalar
z = self.z / scalar
return Vector(x, y, z)
def __abs__(self):
x = self.x
y = self.y
z = self.z
return (x ** 2 + y ** 2 + z ** 2) ** 0.5
Wie man sieht, brauchen wir gar nicht viel Vektorrechnung, nur Addition, Subtraktion, skalare Multiplikation und Division, sowie den Betrag.
Als Nächstes brauchen wir Daten. Die Massen bekommen wir z.B. von Wikipedia, die Orts- und Geschwindigkeitsvektoren aus dem Horizons-System der NASA.
names = []
m = [] # masses
p = [] # positions
v = [] # velocities
object_count = 0
def add_object(name, mass, x, y, z, vx, vy, vz):
global object_count
names.append(name)
m.append(mass)
p.append(Vector(x, y, z))
v.append(Vector(vx, vy, vz))
object_count += 1
add_object(
"Sonne",
1.9885e30,
-1.067706805380953E+06,
-4.182752718194473E+05,
3.086181725476820E+04,
9.312571926520472E-03,
-1.282475570794162E-02,
-1.633507186350417E-04
)
add_object(
"Merkur",
3.3011e23,
-2.052943316123468E+07,
-6.733155053534345E+07,
-3.648992526494771E+06,
3.700430442920571E+01,
-1.117724068132644E+01,
-4.307791469376854E+00
)
add_object(
"Venus",
4.8675e24,
-1.085242008575715E+08,
-5.303290247691983E+06,
6.166496116973171E+06,
1.391218601189967E+00,
-3.515311993215464E+01,
-5.602056890007159E-01
)
# usw...
Nun brauchen wir eine Funktion, die uns die Beschleunigungsvektoren berechnet.
G = 6.67430e-20
def get_accelerations(p):
a = [Vector(0, 0, 0) for i in range(object_count)]
for i in range(object_count):
for j in range(i + 1, object_count):
r = p[j] - p[i]
F = G * m[i] * m[j] * r / abs(r) ** 3
a[i] += F
a[j] -= F
a[i] /= m[i]
return a
Ein paar Anmerkungen dazu:
- Wir gehen alle Paare von Objekten durch, berechnen ihre paarweise Kraft und addieren sie zu einer Gesamtkraft.
- Den Abstandsvektor r berechnen wir einfach nur durch Vektorsubtraktion. Hier zahlt es sich bereits aus, dass wir die Klasse
Vectorgeschrieben haben. - Da wir mit Vektoren rechnen, müssen wir die Vektorform von Newtons Schwerkraftgesetz verwenden.
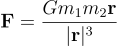
- Wir fügen die Kraft für das erste Objekt zu einer Gesamtkraft hinzu, aber wegen Newtons drittem Gesetz müssen wir dieselbe Kraft von der Gesamtkraft des zweiten Objekts abziehen.
- Um aus der Kraft die Beschleunigung zu ermitteln, teilen wir zum Schluss noch durch die Masse.
Wir bekommen bessere Ergebnisse, wenn wir anstelle der Beschleunigung zu Beginn von Δt die geschätzte Durchschnittsbeschleunigung über den Zeitraum Δt verwenden. Für diese Schätzung verwenden wir das Runge-Kutta-Verfahren, das z.B. hier erklärt wird. Die Kurzfassung lautet: Wir ermitteln vier Zwischenwerte und daraus einen gewichteten Durchschnitt.
Delta_t = 3600
def advance():
# first set of intermediate values
p1 = p
v1 = v
a1 = get_accelerations(p1)
# second set of intermediate values
p2 = object_count * [None]
v2 = object_count * [None]
for i in range(object_count):
p2[i] = p[i] + v1[i] * Delta_t / 2
v2[i] = v[i] + a1[i] * Delta_t / 2
a2 = get_accelerations(p2)
# third set of intermediate values
p3 = object_count * [None]
v3 = object_count * [None]
for i in range(object_count):
p3[i] = p[i] + v2[i] * Delta_t / 2
v3[i] = v[i] + a2[i] * Delta_t / 2
a3 = get_accelerations(p3)
# fourth set of intermediate values
p4 = object_count * [None]
v4 = object_count * [None]
for i in range(object_count):
p4[i] = p[i] + v3[i] * Delta_t
v4[i] = v[i] + a3[i] * Delta_t
a4 = get_accelerations(p4)
# add weighted averages
for i in range(object_count):
p[i] += (v1[i] + 2 * v2[i] + 2 * v3[i] + v4[i]) / 6 * Delta_t
v[i] += (a1[i] + 2 * a2[i] + 2 * a3[i] + a4[i]) / 6 * Delta_t
Der vollständige Code ist hier verfügbar. Ihr benötigt Python 3.x und Pygame. Viel Spaß.