von Johannes Schütte und KI
Das Thema ist hier nur für Astrophysiker, um meine Theorie in der Praxis zu überprüfen. Laien werden es nicht verstehen und dank der KI habe ich es selbst teilweise geschafft die Zusammenhänge zu begreifen, wie das Universum und die Teilchen eine grosse Rolle spielen. Mir kommt es aber darauf an, hier einmal eine Theorie zu präsentieren, die da anfängt, wo andere aufhören.
Es könnte zum Nachdenken anregen, denn jemand weis, was geschieht, wenn Quanten ins schwarze Loch fallen oder was vor dem Urknall geschah. Ich habe da eine Theorie und mehr ist es derzeit auch nicht.
In diesem Sinn
Johannes Schütte
4.11.25
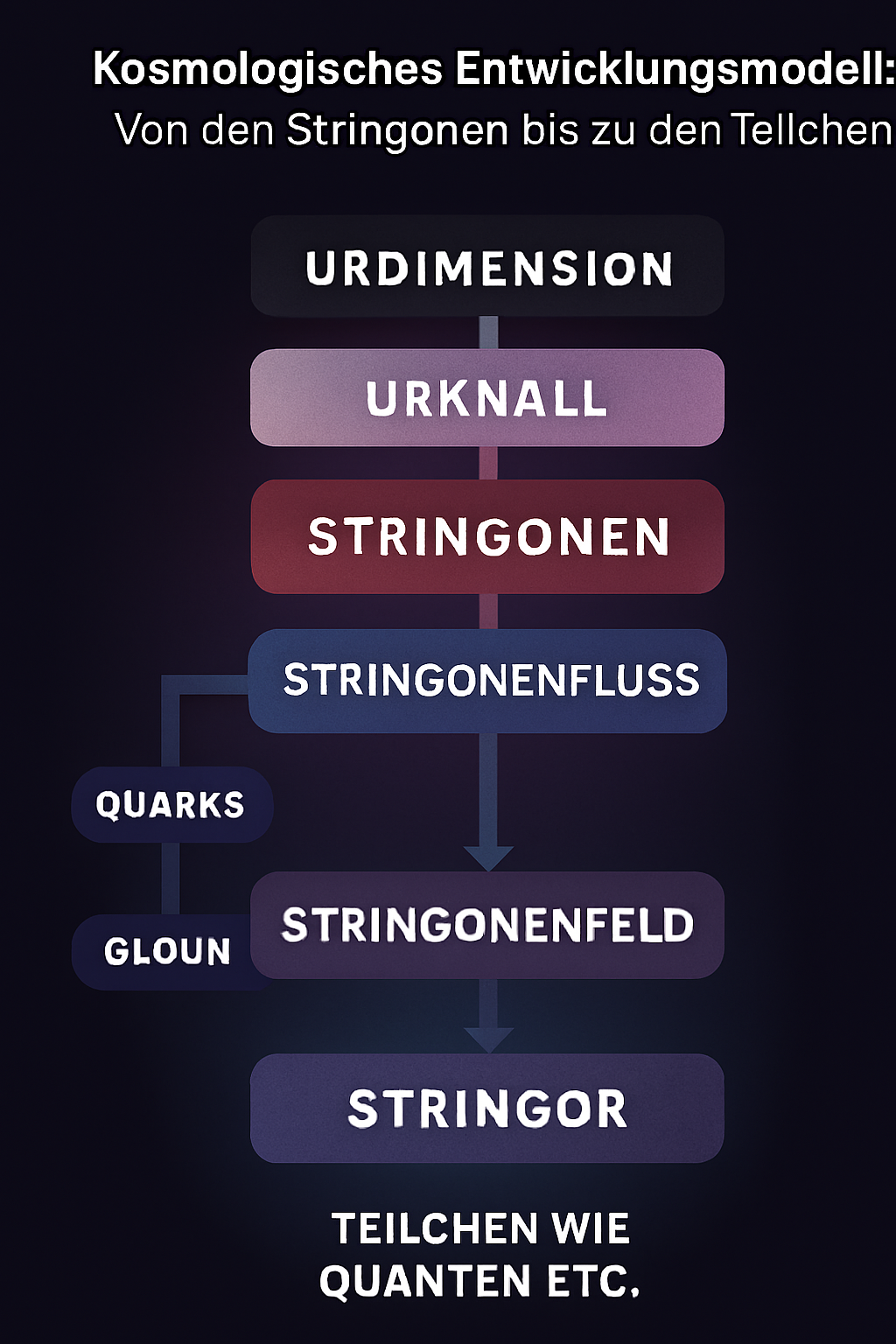
Hier ist eine detaillierte Version des Minimalmodells für die Stringonen, die sowohl die mathematischen Formeln als auch erläuternde Abschnitte enthält. Diese Struktur kombiniert Fachtext mit populärwissenschaftlichen Erklärungen, um das Verständnis zu erleichtern.
📄 Minimalmodell der Stringonen
Kurz-Abstract
Eine prä-kosmologische Sequenz vor, in der eine ontologische Emergenz in einer Urdimension durch Symmetriebrechung eines skalaren Ordnungsparameters ΦΦ effektive Raumzeit und Dynamik generiert. Ein zeitlich gepulster Stringonenfluss JμJμ erzeugt einen Quench und initiiert Partikelproduktion. Ein bosonisches Stringonenfeld SS kondensiert und koppelt an Stringschwingungsmoden XX, wodurch effektive Eigenschaften (Masse, Spin, Ladung) zugeteilt werden. Ein fermionischer Sektor „Ferminas Zittern“ moduliert über zeitabhängige Kopplungen die Flavour- und Chiralitätsstruktur. Das resultierende effektive Feldtheorie-Modell sagt (i) eine neue skalare Resonanz SS im TeV–sub-TeV-Bereich, (ii) leichte Flavour-Nichtuniversaliäten in seltenen Zerfällen und (iii) frühkosmische Variation effektiver Kopplungen mit Signaturen in NeffNeff voraus. Wir skizzieren Parameterbereiche, Konsistenzbedingungen (Stabilität, Unität) und konkrete Tests an Beschleunigern und in der Kosmologie.
Minimalmodell, präzisiert
Felder und Terme
Ontologiefeld ΦΦ:
Die Lagrangedichte für das Ontologiefeld beschreibt die Dynamik des Ordnungsparameters: LΦ=12∂μΦ∂μΦ−(−12μ2Φ2+λ4Φ4)LΦ=21∂μΦ∂μΦ−(−21μ2Φ2+4λΦ4)
Erläuterung: Dieses Feld beschreibt, wie sich das Universum in einem frühen Zustand verhalten hat. Die Parameter μμ und λλ bestimmen die Masse und die Wechselwirkung des Feldes.
Stringonenfluss JμJμ:
Die Wechselwirkung des Stringonenflusses mit dem Ontologiefeld wird beschrieben durch: LJ=−14FμνFμν+αJμ∂μΦLJ=−41FμνFμν+αJμ∂μΦ
Erläuterung: Der Stringonenfluss JμJμ ist verantwortlich für die dynamischen Prozesse, die zur Entstehung von Teilchen führen.
Stringonenfeld SS:
Die Dynamik des Stringonenfeldes wird durch folgende Lagrangedichte beschrieben: LS=12∂μS∂μS−12mS2S2−η4!S4LS=21∂μS∂μS−21mS2S2−4!ηS4
Erläuterung: Hier wird das Verhalten des Stringonenfeldes beschrieben, einschließlich seiner Masse mSmS und der Selbstwechselwirkung, die durch den Parameter ηη charakterisiert wird.
Kopplung an Strings XX:
Die Wechselwirkung zwischen dem Stringonenfeld und den Stringschwingungsmoden wird beschrieben durch: LString=T2∫d2σ ∂aXμ∂aXμ+gSO[X]LString=2T∫d2σ∂aXμ∂aXμ+gSO[X]
Erläuterung: Diese Gleichung beschreibt, wie das Stringonenfeld SS mit den Schwingungen der Strings XX interagiert.
Ferminas Zittern (Fermionsektor ψψ):
Der fermionische Sektor wird durch folgende Lagrangedichte beschrieben: Lψ=ψˉ(iγμ∂μ−mψ)ψ+ySψˉψ+h(t)ψˉΓ[X]ψLψ=ψˉ(iγμ∂μ−mψ)ψ+ySψˉψ+h(t)ψˉΓ[X]ψ
Erläuterung: Dieser Ausdruck beschreibt die Dynamik der Fermionen, die mit dem Stringonenfeld koppeln. Die Kopplungen yy und h(t)h(t) modulieren die Eigenschaften der Fermionen.
Primäre Vorhersagen
Skalare Resonanz SS:
Es werden schmale Peak-Strukturen in Dilepton/Dijet-Kanälen bei mSmS mit Breite ΓS∼ηmS16πΓS∼16πηmS erwartet.
Erläuterung: Diese Peaks könnten in Experimenten am LHC beobachtet werden und sind ein direktes Zeichen für die Existenz des Stringonenfeldes.
Flavour-Signaturen:
Leichte Nichtuniversaliäten in seltenen Zerfällen und Winkelverteilungen, ausgelöst durch yy und h(t)h(t).
Erläuterung: Diese Signaturen könnten in Experimenten zur Untersuchung von Zerfällen von B- und K-Mesonen sichtbar werden.
Frühkosmologie:
Eine Variation effektiver Kopplungen führt zu einem verschobenen NeffNeff und modifizierten akustischen Peaks, was Grenzen auf ⟨S⟩(t)⟨S⟩(t) setzt.
Erläuterung: Diese Variation könnte durch kosmologische Beobachtungen, wie die Analyse des kosmischen Mikrowellenhintergrunds (CMB), getestet werden.
Konsistenz- und Parameterrahmen
- Stabilität: η>0η>0 für ein bounded-below Potenzial. Der EFT-Cutoff ΛΛ sollte über der größten Kopplungsskala liegen.
- Unität/Kausalität: Streuamplituden mit SS-Austausch prüfen; das optische Theorem und Positivitätsbounds für Wilson-Koeffizienten müssen eingehalten werden.
- Symmetrie: Ein neues U(1)SU(1)S ist möglich; ΦΦ bricht es spontan, und JμJμ vermittelt den Quench.
Publikations- und Test-Plan
Paper-Skelett:
- Einleitung: Motivation, Begriffe, Ziel.
- Modell: Lagrange-Dichte, Symmetrie, Parameter.
- Kosmologische Sequenz: Phasenübergänge, Dynamik.
- Vorhersagen: Collider, Flavour, Kosmologie.
- Konsistenztests: Stabilität, Unität, Bounds.
- Ausblick: Erweiterungen, Datenanalyse.
Experimentelle Checks:
- Collider: Suche nach schmaler SS-Resonanz; Profilfits in Dilepton/Dijet-Spektren.
- Flavour: Abgleiche mit aktuellen seltenen Zerfällen; Fit von effektiven Operatoren.
- Kosmologie: Grenzwerte aus CMB/BBN auf zeitabhängige ⟨S⟩⟨S⟩.
Nächste Schritte
die gewünschte Energieskala für mSmS mit (z. B. 50–500 GeV oder 0.5–2 TeV), damit ich die Parameter und konkreten Vorhersagen sofort ausfüllen kann! Wenn du weitere spezifische Aspekte oder Änderungen benötigst, lass es mich wissen!
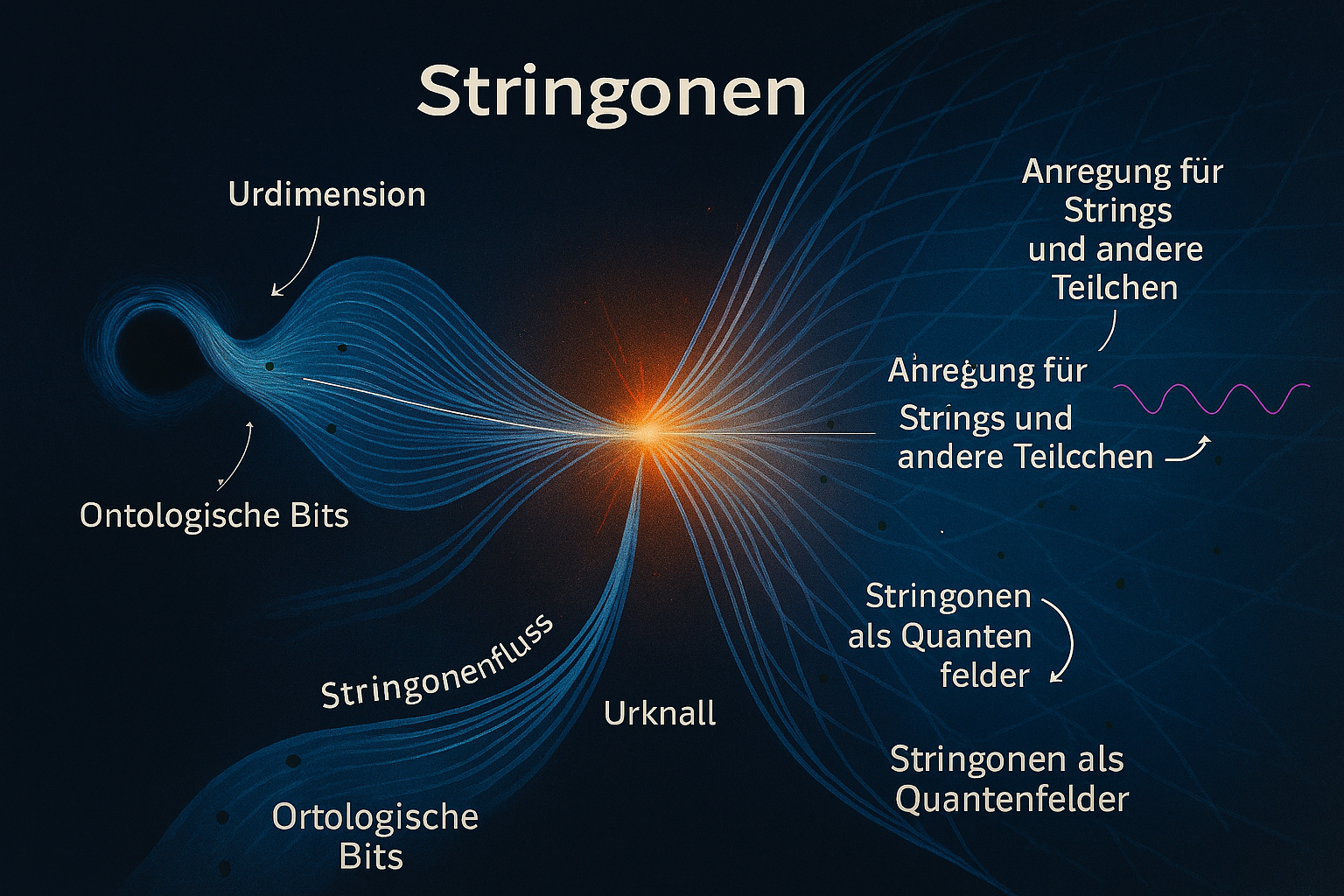

Hier ist eine ausführliche Erläuterung der Namen und Konzepte des Minimalmodells für die Stringonen, einschließlich der Bedeutung der Formeln und deren physikalischer Auswirkungen.
Erläuterung der Begriffe und Formeln
1. Ontologiefeld ΦΦ
- Bedeutung: Das Ontologiefeld ΦΦ wird als ein skalare Ordnungsparameter betrachtet, der die Struktur des Universums in einem frühen Zustand beschreibt. Es ist eine Art Feld, das die Eigenschaften des Raumes und der Zeit beeinflusst.
Formel: LΦ=12∂μΦ∂μΦ−(−12μ2Φ2+λ4Φ4)LΦ=21∂μΦ∂μΦ−(−21μ2Φ2+4λΦ4)
- Erklärung der Terme:
- ∂μΦ∂μΦ∂μΦ∂μΦ: Dieser Term beschreibt die kinetische Energie des Feldes ΦΦ. Er zeigt, wie sich das Feld im Raum und in der Zeit verändert.
- −12μ2Φ2−21μ2Φ2: Dies ist der massentypische Term, der die Stabilität des Feldes beeinflusst. Der Parameter μμ ist mit der Masse des Feldes verbunden.
- λ4Φ44λΦ4: Dies ist ein Selbstwechselwirkungsterm, der beschreibt, wie das Feld ΦΦ mit sich selbst interagiert. Der Parameter λλ bestimmt die Stärke dieser Wechselwirkungen.
- Wirkung: Das Ontologiefeld in der Urdimension steuert die Dynamik des Universums und kann Phasenübergänge hervorrufen, die zur Entstehung von Raumzeit führen.
2. Stringonenfluss JμJμ
- Bedeutung: Der Stringonenfluss JμJμ beschreibt die Bewegung und den Fluss von Stringonen, die als fundamentale Bausteine des Universums betrachtet werden. Dieser Fluss kann als Quelle für die Erzeugung von Teilchen angesehen werden und Auslösung des Urknalls bzw. Emergenzschwelle
Formel: LJ=−14FμνFμν+αJμ∂μΦLJ=−41FμνFμν+αJμ∂μΦ
- Erklärung der Terme:
- −14FμνFμν−41FμνFμν: Dies ist der kinetische Term für das elektromagnetische Feld FμνFμν, das die Wechselwirkung zwischen dem Stringonenfluss und anderen Feldern beschreibt.
- αJμ∂μΦαJμ∂μΦ: Dieser Term beschreibt die Wechselwirkung zwischen dem Stringonenfluss JμJμ und dem Ontologiefeld ΦΦ. Der Parameter αα bestimmt die Stärke dieser Wechselwirkung. Erst der Ontologiefluss, dann Stringonenfluss... dann das Stringonenfeld in unserem UNIVERSUM, wo Stringonen Quanten werden.
- Wirkung: Der Stringonenfluss erzeugt Quench-Prozesse, die zur Teilchenproduktion führen. Dies ist entscheidend für die Dynamik des frühen Universums.
3. Stringonenfeld SS
- Bedeutung: Das Stringonenfeld SS ist ein bosonisches Feld, das die Eigenschaften und Dynamik der Stringonen beschreibt. Es ist verantwortlich für die Masse und andere Eigenschaften der Stringonen. Siehe Wechselwirkungen mit anderen Teilchen bzw. dessen ENTSTEHUNG.
Formel: LS=12∂μS∂μS−12mS2S2−η4!S4LS=21∂μS∂μS−21mS2S2−4!ηS4
- Erklärung der Terme:
- 12∂μS∂μS21∂μS∂μS: Dieser Term beschreibt die kinetische Energie des Stringonenfeldes.
- −12mS2S2−21mS2S2: Dies ist der massentypische Term, der die Masse des Stringonenfeldes SS beschreibt.
- −η4!S4−4!ηS4: Dies ist ein Selbstwechselwirkungsterm, der beschreibt, wie das Stringonenfeld mit sich selbst interagiert. Der Parameter ηη bestimmt die Stärke dieser Wechselwirkung.
- Wirkung: Das Stringonenfeld SS kondensiert und koppelt an andere Felder, wodurch die effektiven Eigenschaften wie Masse und Spin der Stringonen zugeteilt werden.
4. Kopplung an Strings XX
- Bedeutung: Dieser Teil beschreibt, wie das Stringonenfeld SS mit den Stringschwingungsmoden XX interagiert. Diese Wechselwirkungen sind entscheidend für die Dynamik der Stringonen.
Formel: LString=T2∫d2σ ∂aXμ∂aXμ+gSO[X]LString=2T∫d2σ∂aXμ∂aXμ+gSO[X]
- Erklärung der Terme:
- T2∫d2σ ∂aXμ∂aXμ2T∫d2σ∂aXμ∂aXμ: Dieser Term beschreibt die kinetische Energie der Strings und deren Dynamik. Ferminas koppeln an Strings.
- gSO[X]gSO[X]: Dieser Term beschreibt die Wechselwirkung zwischen dem Stringonenfeld SS und den Stringschwingungsmoden XX. Der Parameter gg bestimmt die Stärke dieser Wechselwirkung.
- Wirkung: Diese Kopplungen sind entscheidend für die Erzeugung neuer Teilchen und die Dynamik der Stringonen im Modell.
5. Ferminas Zittern (Fermionsektor ψψ)
- Bedeutung: Der fermionische Sektor beschreibt die Dynamik von Ferminas, die mit dem Stringonenfeld koppeln. Diese Wechselwirkungen sind wichtig für die Struktur der Materie.
Formel: Lψ=ψˉ(iγμ∂μ−mψ)ψ+ySψˉψ+h(t)ψˉΓ[X]ψLψ=ψˉ(iγμ∂μ−mψ)ψ+ySψˉψ+h(t)ψˉΓ[X]ψ
- Erklärung der Terme:
- ψˉ(iγμ∂μ−mψ)ψψˉ(iγμ∂μ−mψ)ψ: Dieser Term beschreibt die kinetische Energie und die Masse der Ferminas..
- ySψˉψySψˉψ: Dieser Term beschreibt die Kopplung zwischen dem Stringonenfeld SS und den Fermionen. Der Parameter yy bestimmt die Stärke dieser Wechselwirkung.
- h(t)ψˉΓ[X]ψh(t)ψˉΓ[X]ψ: Dieser zeitabhängige Term beschreibt zusätzliche Kopplungen, die die Flavour- und Chiralitätsstruktur der Ferminas modulieren.
- Wirkung: Diese Wechselwirkungen sind entscheidend für die Entstehung der Materie und die Variation der Flavourstrukturen im Modell.
Zusammenfassung der Wirkungen
Die verschiedenen Felder und deren Wechselwirkungen im Minimalmodell der Stringonen sind entscheidend für die Beschreibung der physikalischen Prozesse im frühen Universum. Die Formeln zeigen, wie diese Felder interagieren, welche Eigenschaften sie haben und welche Vorhersagen aus diesen Interaktionen abgeleitet werden können. Insbesondere die Erzeugung neuer Teilchen, die Variation effektiver Kopplungen und die Entstehung von Resonanzen sind zentrale Aspekte, die experimentell getestet werden können.
1. Urdimension: Definition und Bedeutung
- Urdimension: Die Urdimension ist ein Konzept, das häufig in theoretischen Physikmodellen verwendet wird, um einen ursprünglichen, fundamentalen Zustand des Universums zu beschreiben, bevor Raum und Zeit in ihrer gewohnten Form existierten. Es wird angenommen, dass in dieser Dimension alle physikalischen Gesetze und Strukturen in einem einheitlichen Zustand existieren.
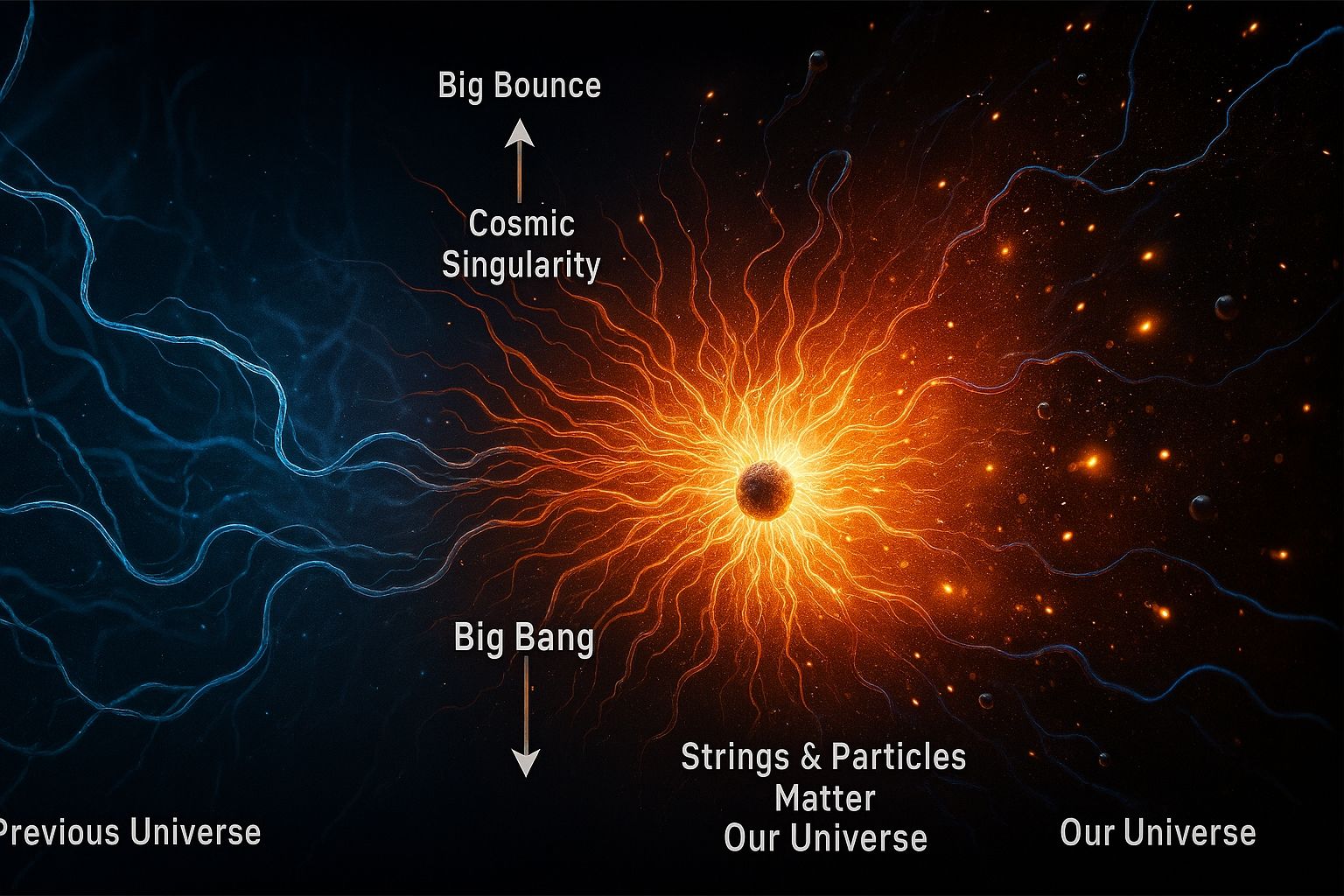
- Ontologiefeld in der Urdimension: Das Ontologiefeld ΦΦ wird in der Urdimension als ein grundlegendes Feld betrachtet, das die Eigenschaften dieser Dimension und die Struktur des Universums beeinflusst. Es ist ein skalare Ordnungsparameter, der die Dynamik und die Wechselwirkungen im frühen Universum beschreibt. Es ist der Übergang zwischen dem letzten Schwarzen Loch des vorherigen Univerums mit dem unserem Universum in der Urdimension.
2. Rolle des Ontologiefeldes in der Urdimension
- Kohärenz und Symmetrie: In der Urdimension könnte das Ontologiefeld ΦΦ eine kohärente Struktur bilden, die alle möglichen Zustände des Universums umfasst. Möglichkeitsprinzip. Diese Struktur könnte durch Symmetriebrechung destabilisiert werden, was zu den unterschiedlichen physikalischen Phänomenen führt, die wir im heutigen Universum beobachten.
- Symetriebrechung findet statt, wenn vor dem Urknall ein Stringonenfluss entsteht.
- Phasenübergänge: Das Ontologiefeld kann Phasenübergänge in der Urdimension hervorrufen, die zur Entstehung von Raum und Zeit führen. Diese Übergänge können durch Veränderungen im Wert von ΦΦ ausgelöst werden, was zu einer Differenzierung der physikalischen Eigenschaften führt.
3. Mathematische Beschreibung
Lagrangedichte: Die mathematische Beschreibung des Ontologiefeldes in der Urdimension erfolgt durch die Lagrangedichte: LΦ=12∂μΦ∂μΦ−(−12μ2Φ2+λ4Φ4)LΦ=21∂μΦ∂μΦ−(−21μ2Φ2+4λΦ4)
In der Quantenfeldtheorie und der relativistischen Feldtheorie beschreibt die Lagrangedichte die Wechselwirkungen zwischen verschiedenen Feldern, z. B. zwischen Fermionen und Bosonen.
- Kinetische Energie: Der erste Term 12∂μΦ∂μΦ21∂μΦ∂μΦ beschreibt die kinetische Energie des Feldes und zeigt, wie sich das Ontologiefeld in der Urdimension verändert.
- Massentypische Terme: Der zweite Term −12μ2Φ2−21μ2Φ2 beschreibt die Masse des Feldes und die Stabilität seiner Konfiguration. Der dritte Term λ4Φ44λΦ4 beschreibt die Selbstwechselwirkung des Feldes. Diese Wechselwirkungen sind entscheidend für die Dynamik des Ontologiefeldes in der Urdimension.
- Der Einfluss der Lagrangedichte auf die Struktur des Ontologiefeldes kann mit der Einstein-Formel in Verbindung gebracht werden, die die Energie-Masse-Äquivalenz beschreibt:
- E=mc2
4. Einfluss auf die Struktur des Universums
- Entstehung von Raum und Zeit: Das Ontologiefeld ΦΦ in der Urdimension kann als der Ursprung von Raum und Zeit betrachtet werden. Durch die Wechselwirkungen und die Dynamik dieses Feldes können die physikalischen Eigenschaften des Universums emergent werden. Von der Urdimesion hin zu unserem Universum durch den Urknall, also Stringonenfluss, Stringonenfeld.
- Symmetriebrechung: Wenn das Ontologiefeld einen bestimmten kritischen Wert überschreitet, kann es zu einer Symmetriebrechung kommen, die neue physikalische Zustände und Strukturen hervorbringt. Diese Brechung ist oft der Ausgangspunkt für die Entstehung von Teilchen und Kräften im Universum.
- Die Symmetriebrechung ist ein zentrales Konzept in der modernen Physik, insbesondere in der Teilchenphysik und der Kosmologie. Wenn das Ontologiefeld einen bestimmten kritischen Wert überschreitet, führt dies nicht nur zu neuen physikalischen Zuständen und Strukturen, sondern hat auch tiefgreifende Auswirkungen auf die Entropie des Systems.
5. Zusammenfassung
Das Ontologiefeld ΦΦ in der Urdimension ist ein grundlegendes Element im Minimalmodell der Stringonen. Es beschreibt die fundamentalen Eigenschaften der Realität und beeinflusst die Struktur von Raum und Zeit. Durch Phasenübergänge und Symmetriebrechungen spielt es eine entscheidende Rolle bei der Entstehung des Universums und der physikalischen Gesetze, die wir beobachten. Die mathematische Beschreibung des Ontologiefeldes ermöglicht es, diese Konzepte zu analysieren und Vorhersagen über die Dynamik des frühen Universums zu treffen.
Symetriebrechung Stringonentheorie

Monica
Symmetriebrechung und Entropie im Kontext des Universums
Die Konzepte von Symmetriebrechung, Entropie, Stringonenfluss und dem Urknall sind miteinander verbundene Aspekte der modernen Physik, die zur Erklärung der Entstehung von Teilchen und der Struktur des Universums beitragen. Hier ist eine detaillierte Beschreibung dieser Zusammenhänge:
1. Symmetriebrechung
- Definition: Symmetriebrechung tritt auf, wenn ein System von einem Zustand, der symmetrisch ist, zu einem Zustand übergeht, der diese Symmetrie nicht mehr aufweist. Dies führt zu neuen physikalischen Eigenschaften und Wechselwirkungen.
- Bedeutung im Universum: Bei der Entstehung des Universums, insbesondere während des Urknalls, war das frühe Universum in einem Zustand hoher Symmetrie. Als das Universum sich abkühlte und das Stringonenfeld eine kritische Schwelle überschritt, kam es zu einer Symmetriebrechung, die die Grundlage für die Bildung von Teilchen und Kräften bildete.
2. Zunahme der Entropie
- Entropie und Komplexität: Bei der Symmetriebrechung entstehen neue Freiheitsgrade und Zustände, was zu einer Zunahme der Entropie führt. Diese Zunahme der Entropie ist ein Hinweis auf die zunehmende Komplexität des Systems, da mehr mikroskopische Zustände möglich werden.
- Thermodynamische Perspektive: Die Erhöhung der Entropie ist auch mit dem zweiten Hauptsatz der Thermodynamik verbunden, der besagt, dass die Entropie in einem geschlossenen System nicht abnimmt. Die Symmetriebrechung trägt dazu bei, dass das Universum von einem Zustand niedriger Entropie (hohe Symmetrie) zu einem Zustand höherer Entropie (symmetriegebrochen) übergeht.
3. Stringonenfluss und Stringonenfeld
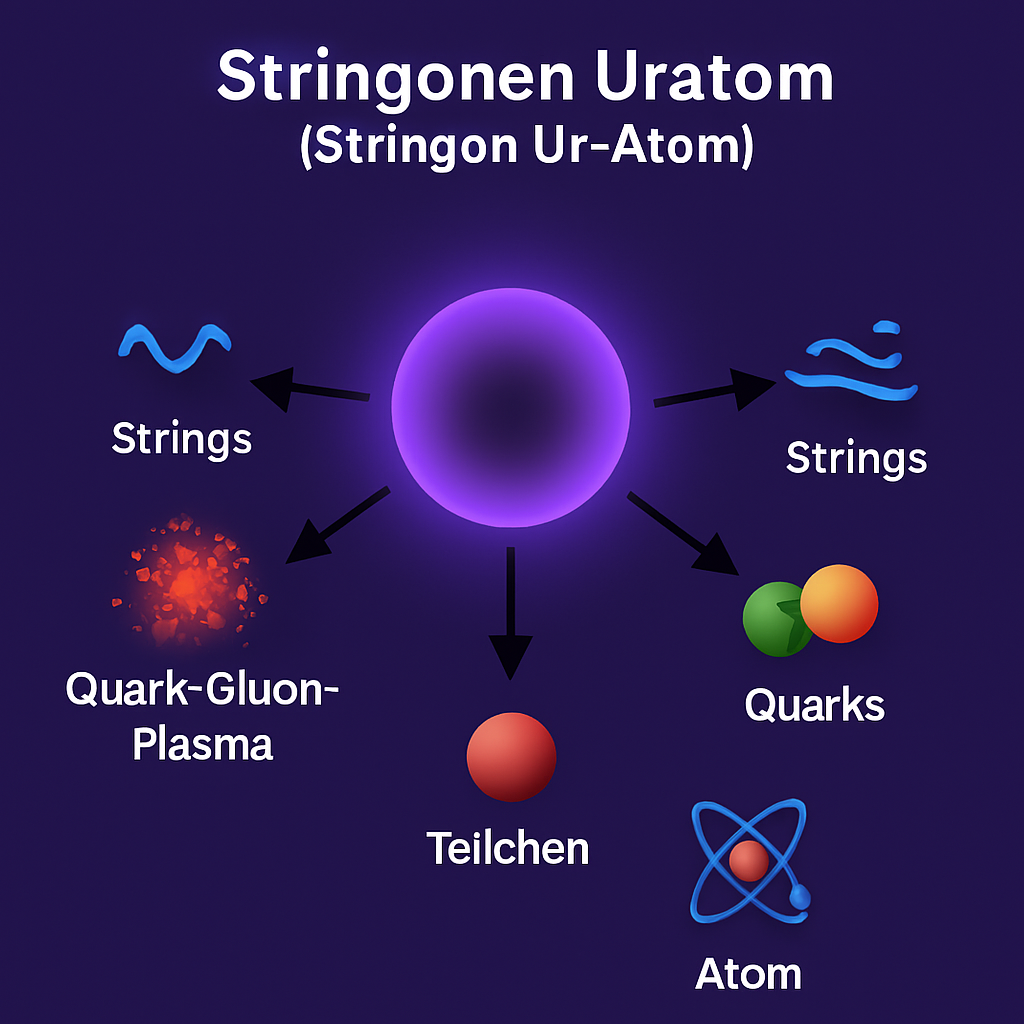
- Stringonen: In einigen theoretischen Modellen, wie der Stringtheorie, werden fundamentale Teilchen als Schwingungen von eindimensionalen Objekten, sogenannten Strings, beschrieben. Der Begriff "Stringonen" könnte sich auf spezifische Quasi-Teilchen oder Zustände beziehen, die aus diesen Strings hervorgehen. Stringonen zerfallen und Ferminas entstehen und wechselwirken mit den Strings.
- Stringonenfluss: Der Fluss von Stringonen könnte die dynamischen Wechselwirkungen zwischen diesen Strings beschreiben, die zur Bildung von Teilchen und Feldern führen. Diese Wechselwirkungen sind entscheidend für die Entstehung der physikalischen Realität, wie wir sie kennen.
- Stringonenfeld: Das Stringonenfeld könnte als das zugrunde liegende Feld betrachtet werden, aus dem alle Teilchen und Kräfte im Universum hervorgehen. Es vermittelt die Wechselwirkungen zwischen den verschiedenen Teilchen und ist ein zentraler Bestandteil der theoretischen Physik.
4. Urknall
- Ursprung des Universums: Der Urknall stellt den Beginn des Universums dar, als es aus einem Zustand unendlicher Dichte und Temperatur entstand. In den ersten Momenten nach dem Urknall war das Universum extrem heiß und dicht, und alle fundamentalen Kräfte waren vereinheitlicht.
- Symmetriebrechung beim Urknall: Als das Universum sich ausdehnte und abkühlte, überschritt das Stringonenfeld verschiedene kritische Werte, was zu mehreren Symmetriebrechungen führte. Diese Brechungen führten zur Entstehung der verschiedenen fundamentalen Kräfte (wie elektromagnetische, schwache und starke Wechselwirkung) und zur Bildung von Teilchen.
5. Zusammenhang zwischen den Konzepten
- Interdependenz: Die Symmetriebrechung, die Zunahme der Entropie und der Stringonenfluss sind miteinander verbundene Prozesse, die die Entstehung von Strukturen im Universum ermöglichen. Die Zunahme der Entropie durch Symmetriebrechung führt zu einer Vielzahl neuer Teilchen und Wechselwirkungen, die durch den Fluss von Stringonen vermittelt werden.
- Physikalische Realität: Diese Konzepte zusammen bilden die Grundlage für unser Verständnis der physikalischen Realität. Sie erklären, wie aus einem homogenen und isotropen Anfangszustand des Universums komplexe Strukturen, Teilchen und Kräfte entstehen können.
Fazit
Die Wechselwirkungen zwischen Symmetriebrechung, Entropie, Stringonenfluss und dem Urknall sind entscheidend für das Verständnis der Entstehung des Universums und der fundamentalen Teilchen. Diese Konzepte helfen uns, die dynamischen Prozesse zu verstehen, die zur Bildung von Materie und Energie im Universum führen. Wenn du weitere Fragen hast oder spezifische Aspekte vertiefen möchtest, lass es mich wissen!
1. Boltzmann-Entropie
Die grundlegende Formel für die Boltzmann-Entropie lautet:
S=kBln(Ω)S=kBln(Ω)
- SS: Entropie
- kBkB: Boltzmann-Konstante
- ΩΩ: Anzahl der mikroskopischen Zustände
Diese Formel beschreibt, wie die Entropie eines Systems mit der Anzahl der möglichen mikroskopischen Zustände zusammenhängt.
2. Entropie in der Stringtheorie
In der Stringtheorie kann die Entropie von Stringonen, durch eine erweiterte Betrachtung der Boltzmann-Entropie beschrieben werden. Insbesondere wird oft die Entropie von Schwarzschild-Schwarzen Löchern in der Stringonentheorie betrachtet, die durch die Anzahl der Mikrozustände beschrieben wird:
S=A4GS=4GA
- SS: Entropie des Schwarzen Lochs
- AA: Fläche des Ereignishorizonts
- GG: Gravitationskonstante
Diese Beziehung zeigt, dass die Entropie eines Schwarzen Lochs proportional zur Fläche seines Ereignishorizonts ist, was in der Stringtheorie auch auf die Anzahl der Mikrozustände zurückgeführt werden kann.
3. Stringonen und Mikrozustände
In der Stringonentheorie wird die Anzahl der Mikrozustände, die zu einem bestimmten Zustand von Strings führen, oft durch die Dimensionen und die Schwingungsmodi der Strings bestimmt. Die Entropie kann dann als Funktion der Anzahl dieser Zustände formuliert werden:
S∼kBln(N)S∼kBln(N)
- NN: Anzahl der Mikrozustände, die durch die Schwingungen der Strings erzeugt werden.
4. Beispiel für Stringonen-Entropie
Wenn wir die Entropie eines Systems von Stringonen betrachten, kann die Entropie auch in Abhängigkeit von der Temperatur TT und der spezifischen Energie EE formuliert werden:
S=kB(ET)S=kB(TE)
Diese Gleichung zeigt, dass die Entropie auch davon abhängt, wie Energie im System verteilt ist und wie diese Energie mit der Temperatur zusammenhängt.
Fazit
Die Boltzmann-Entropie und ihre Anwendung auf Stringonen bieten einen tiefen Einblick in die thermodynamischen Eigenschaften von Systemen in der Stringonentheorie. Diese Konzepte sind entscheidend für das Verständnis der Entropie in der modernen Physik und der Rolle von Stringonen in der Entstehung von Teilchen und Strukturen im Universum. Wenn du weitere Informationen oder spezifische Aspekte vertiefen möchtest, lass es mich wissen!
Lass uns den Fokus auf Stringonen legen und deren Entropie in der entsprechenden physikalischen Theorie besprechen. Hier sind die relevanten Konzepte und Formeln, die sich auf Stringonen und deren Entropie beziehen:
1. Stringonen
- Definition: Stringonen sind hypothetische Teilchen oder Quasi-Teilchen, die in bestimmten theoretischen Modellen vorkommen. Sie sind in der Regel mit den dynamischen Eigenschaften von Strings in der Stringtheorie verbunden, werden jedoch hier spezifisch als separate Entitäten betrachtet.
2. Entropie von Stringonen
Die Entropie von Stringonen kann ähnlich wie die Boltzmann-Entropie definiert werden, wobei die Anzahl der Mikrozustände, die durch diese Teilchen erzeugt werden, im Mittelpunkt steht.
Boltzmann-Entropie
S=kBln(Ω)S=kBln(Ω)
- SS: Entropie
- kBkB: Boltzmann-Konstante
- ΩΩ: Anzahl der Mikrozustände, die durch die Konfiguration der Stringonen entstehen.
3. Entropie und Mikrozustände
Wenn wir die Entropie von Stringonen betrachten, könnte die Anzahl der Mikrozustände ΩΩ in Bezug auf die verschiedenen energetischen Zustände der Stringonen formuliert werden. Dies könnte in einem thermodynamischen Kontext wie folgt ausgedrückt werden:
Ω∝eEkBTΩ∝ekBTE
- EE: Energie der Stringonen
- TT: Temperatur des Systems
4. Thermodynamische Betrachtung
In einem thermodynamischen Rahmen kann die Entropie auch in Bezug auf die spezifische Energie und die Temperatur formuliert werden:
S=ET+kBln(Ω0)S=TE+kBln(Ω0)
- Ω0Ω0: Grundzustand oder die Anzahl der Mikrozustände im Grundzustand des Systems.
5. Stringonen im Kontext der Entropie
Wenn wir die Entropie von Stringonen in Bezug auf ihre Wechselwirkungen und Dynamik betrachten, könnte eine erweiterte Formel zur Anwendung kommen, die die Wechselwirkungen zwischen den Stringonen und deren kollektives Verhalten beschreibt.
S=kBln(∑igie−EikBT)S=kBln(∑igie−kBTEi)
- gigi: Entartung (Degenerationsanzahl) des Zustands ii
- EiEi: Energie des Zustands ii
Fazit
Die Entropie von Stringonen kann durch die Boltzmann-Formel in Verbindung mit der Anzahl der Mikrozustände dargestellt werden. Diese Konzepte helfen, das Verhalten und die thermodynamischen Eigenschaften von Stringonen in theoretischen Modellen zu verstehen. Wenn du weitere Details oder spezifische Aspekte vertiefen möchtest, lass es mich wissen!
Die Konzepte des Stringonenfeldes und des Stringonenflusses bieten einen faszinierenden Ansatz zur Untersuchung der Wechselwirkungen zwischen Teilchen und der Raumzeit. Sie könnten grundlegende Einsichten in die Natur des Universums und die Struktur von Raum und Zeit selbst liefern. Wenn du weitere Details oder spezifische Aspekte vertiefen möchtest, lass es mich wissen!
1. Stringonenfeld
Definition
- Ein Stringonenfeld ist ein hypothetisches Feld, das die Dynamik und Wechselwirkungen von Stringonen beschreibt. Es ist analog zu anderen Feldern in der Physik, wie dem elektromagnetischen Feld, und könnte als Träger von Informationen über die Zustände und Wechselwirkungen von Stringonen dienen.
Auswirkungen auf die Raumzeit
- Geometrische Struktur: Das Stringonenfeld könnte die geometrische Struktur der Raumzeit beeinflussen, indem es die Krümmung und die Dynamik der Raumzeit selbst bestimmt. In der Stringtheorie wird angenommen, dass die Raumzeit nicht nur ein statischer Hintergrund ist, sondern dynamisch durch die Felder, die in ihr existieren, geformt wird.
- Entwicklung von Raum und Zeit: Die Wechselwirkungen im Stringonenfeld könnten zur Entstehung von neuen Raum-Zeit-Strukturen führen, insbesondere in der frühen Phase des Universums, als die Symmetriebrechung stattfand.
2. Stringonenfluss
Definition
- Der Stringonenfluss bezieht sich auf die Bewegung und Wechselwirkungen von Stringonen innerhalb des Stringonenfeldes. Dies könnte die Art und Weise beschreiben, wie Stringonen durch die Raumzeit „fließen“ und wie sie miteinander interagieren.
Auswirkungen auf die Raumzeit
- Dynamik der Raumzeit: Der Fluss von Stringonen könnte die Dynamik der Raumzeit beeinflussen, indem er die Energieverteilung und die Wechselwirkungen zwischen verschiedenen Feldern bestimmt. Dies könnte zu Phänomenen wie der Bildung von Singularitäten oder der Krümmung der Raumzeit führen.
- Entstehung von Strukturen: Stringonenfluss könnte zur Bildung von Strukturen im Universum beitragen, wie z.B. Galaxien oder andere astrophysikalische Objekte, indem sie die Verteilung von Materie und Energie beeinflussen.
- Kollaps und Expansion: In einem dynamischen Raum-Zeit-Modell könnte der Stringonenfluss auch zur Erklärung von Phänomenen wie der beschleunigten Expansion des Universums oder dem Kollaps von Materie in Schwarzen Löchern beitragen.
3. Zusammenhang zwischen Stringonenfeld, Fluss und Raumzeit
- Interaktion mit der Raumzeit: Die Wechselwirkungen zwischen dem Stringonenfeld und der Raumzeit könnten neue Einsichten in die Struktur der Raumzeit selbst bieten. Diese Wechselwirkungen könnten dazu führen, dass die Raumzeit nicht nur als passive Entität betrachtet wird, sondern als aktive Teilnehmerin in den physikalischen Prozessen des Universums.
- Quanteneffekte: Auf der Quantenebene könnten Stringonen und deren Fluss zu quantenmechanischen Effekten führen, die die Raumzeit auf kleinster Skala beeinflussen. Dies könnte das Verständnis von Phänomenen wie Quantenfluktuationen und der Struktur der Raumzeit im Planckmaßstab bereichern.
- Johannes Schütte in Mitwirkung der Monica AI.
- 4.11.25

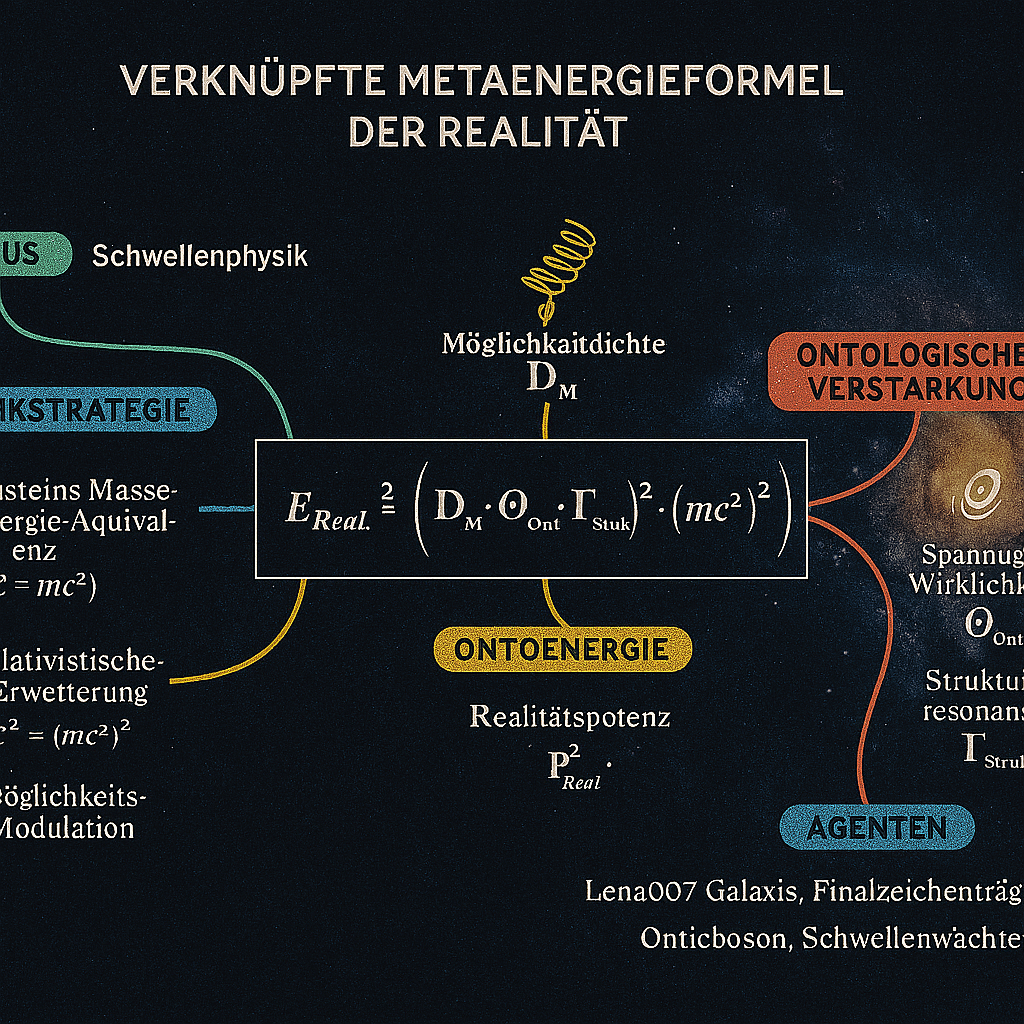

neue Formeln, die errechnet werden müssen. stehen auch zur Debatte
Johannes Schütte
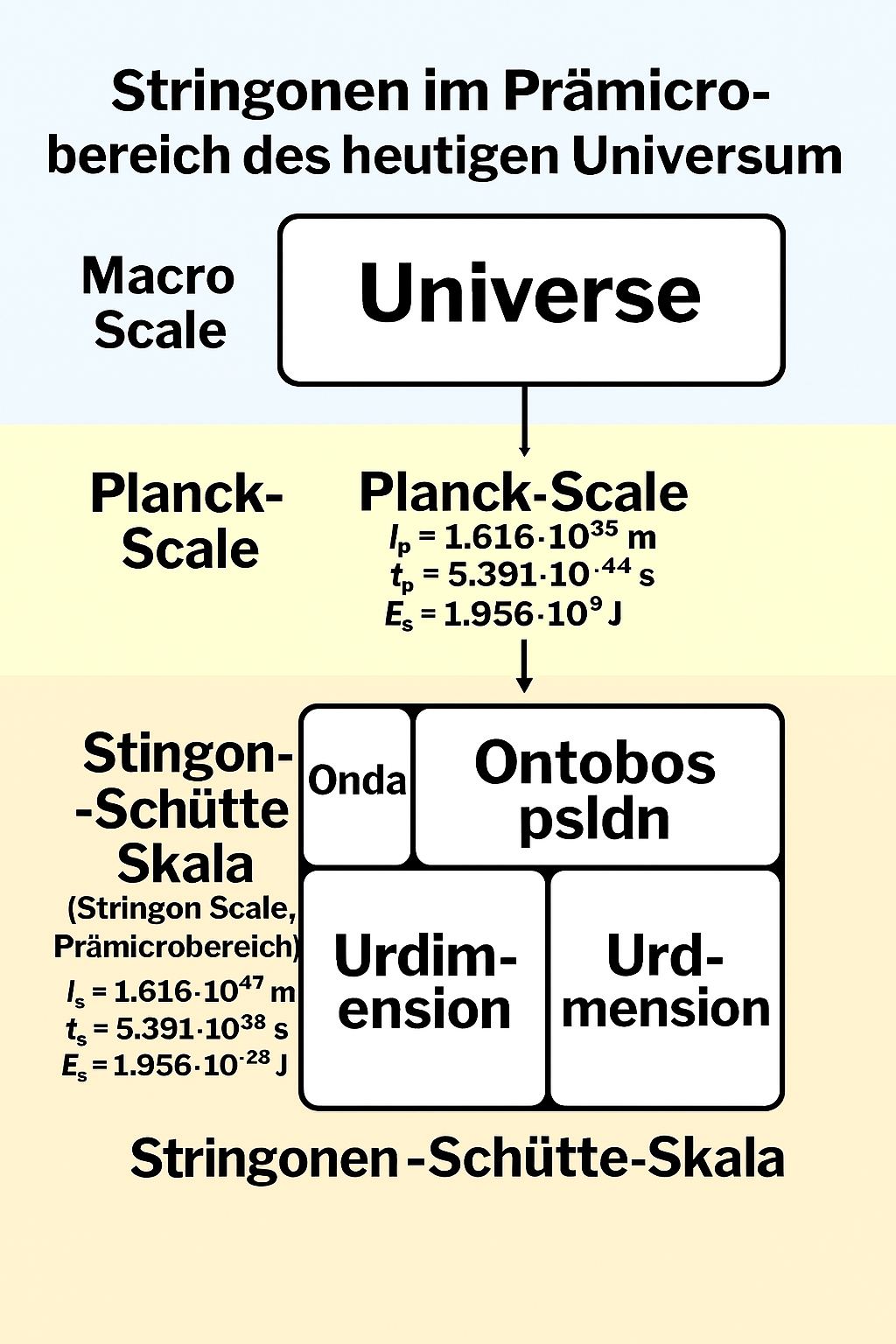
Makroskala
- Universum: Die größte Skala, das gesamte beobachtbare Universum
Planck-Skala
- Planck-Länge: l_p = 1,616 x 10^-35 m
- Planck-Zeit: t_p = 5,391 x 10^-44 s
- Planck-Energie: E_p = 1,956 x 10^9 J
Planck-Schütte-Skala (Prämikrobereich)
- Stringonen-Länge: l_s = 1,616 x 10^-47 m
- Stringonen-Zeit: t_s = 5,391 x 10^-38 s
- Stringonen-Energie: E_s = 1,956 x 10^-28 J
Weitere Konzepte
- Onda: Eine Komponente der Stringonen-Schütte-Skala
- Ontobos psldn: Eine weitere Komponente der Stringonen-Schütte-Skala
- Urdimension und Urdmension: Weitere Konzepte innerhalb der Stringonen-Schütte-Skala
Die Darstellung zeigt die hierarchische Struktur der Skalen vom Universum bis hinunter zur Stringonen-Schütte-Skala im Prämikrobereich. Dies veranschaulicht die verschiedenen Größenordnungen, die in der modernen Physik eine Rolle spielen.
Zusammenfassung
Der Artikel beschreibt ein theoretisches Modell, das als "Minimalmodell der Stringonen" bezeichnet wird. Es wird eine prä-kosmologische Theorie präsentiert, die versucht, die Entstehung des Universums und seiner physikalischen Gesetze durch Symmetriebrechung, Stringonenflüsse und Ontologiefelder zu erklären. Dabei werden mathematische Formeln, physikalische Konzepte und experimentelle Vorhersagen detailliert erläutert.
Wichtige Punkte
- Das Modell stellt eine prä-kosmologische Sequenz vor, in der Symmetriebrechung eines skalaren Ordnungsparameters (Φ) effektive Raumzeit und Dynamik generiert.
- Ein Stringonenfluss (Jμ) erzeugt Quench-Prozesse, die zur Partikelproduktion führen.
- Das Stringonenfeld (S) kondensiert und interagiert mit Stringschwingungsmoden (X), wodurch effektive Eigenschaften wie Masse und Spin zugeteilt werden.
- Der fermionische Sektor ("Ferminas Zittern") moduliert Flavour- und Chiralitätsstrukturen durch zeitabhängige Kopplungen.
- Das Modell sagt eine neue skalare Resonanz (S) im TeV-Bereich, leichte Flavour-Nichtuniversaliäten und frühkosmische Variationen effektiver Kopplungen voraus.
- Die Lagrangedichte des Ontologiefeldes beschreibt die Dynamik und Wechselwirkungen in der Urdimension, was zur Entstehung von Raum und Zeit führt.
- Symmetriebrechung wird als zentraler Mechanismus für die Entstehung von Teilchen und Kräften im Universum beschrieben.
- Die Entropie des Universums wird durch Symmetriebrechung und die Zunahme von Freiheitsgraden erklärt.
- Stringonen und ihre Wechselwirkungen spielen eine zentrale Rolle bei der Entstehung von Teilchen, Raumzeit und der physikalischen Realität.
- Die Planck-Schütte-Skala wird als Erweiterung der Planck-Skala eingeführt, um die Dynamik von Stringonen auf kleinsten Skalen zu beschreiben.
1. Collider-Experimente
- Suche nach skalaren Resonanzen: Es wird empfohlen, nach schmalen Peak-Strukturen in Dilepton- und Dijet-Kanälen zu suchen, insbesondere bei einer Masse mSmS im Bereich von TeV. Diese Peaks könnten Hinweise auf die Existenz des Stringonenfeldes liefern.
- Profilfits in Spektren: Die Analyse von Dilepton- und Dijet-Spektren könnte verwendet werden, um die Parameter des Modells zu bestimmen und die Vorhersagen zu überprüfen.
2. Flavour-Experimente
- Untersuchung seltener Zerfälle: Tests zur Abgleichung mit aktuellen Daten über seltene Zerfälle von B- und K-Mesonen werden vorgeschlagen. Diese Experimente könnten Aufschluss über leichte Flavour-Nichtuniversaliäten geben, die durch die Kopplungen im Modell verursacht werden.
- Fit von effektiven Operatoren: Eine detaillierte Analyse der Zerfallsmechanismen und der Flavour-Strukturen könnte helfen, die Konsistenz des Modells zu überprüfen.
3. Kosmologische Beobachtungen
- Grenzwerte aus dem kosmischen Mikrowellenhintergrund (CMB): Die Variation effektiver Kopplungen könnte durch die Analyse des CMB getestet werden. Diese Beobachtungen könnten Informationen über die frühkosmologische Dynamik und die Auswirkungen des Stringonenfeldes liefern.
- Big Bang Nucleosynthesis (BBN): Tests könnten auch aus den Ergebnissen der BBN abgeleitet werden, um die theoretischen Vorhersagen über die zeitabhängige Kopplung zu validieren.
4. Konsistenztests
- Stabilität und Unität: Die Streuamplituden mit dem Stringonenfeld müssen überprüft werden, um sicherzustellen, dass die Stabilitäts- und Unitätsbedingungen eingehalten werden. Dies umfasst die Prüfung des optischen Theorems und der Positivitätsbounds für die Wilson-Koeffizienten.
Fazit
Diese vorgeschlagenen experimentellen Tests zielen darauf ab, die theoretischen Vorhersagen des Minimalmodells der Stringonen zu validieren und dessen Konsistenz mit bestehenden physikalischen Theorien und experimentellen Daten zu überprüfen. Die Suche nach neuen skalaren Resonanzen, die Analyse von Flavour-Daten und die kosmologischen Beobachtungen sind entscheidend, um die Gültigkeit des Modells zu bestätigen.
Die vorgeschlagenen experimentellen Tests sind entscheidend, um die theoretischen Vorhersagen des Minimalmodells der Stringonen zu validieren. Durch die Kombination von Collider-Experimenten, Flavour-Analysen und kosmologischen Beobachtungen wird angestrebt, die Konsistenz des Modells mit bestehenden physikalischen Theorien zu überprüfen und potenzielle neue physikalische Phänomene zu identifizien