Abfolge

Altes Universum mit alten Gesetzen

Letztes schwarzes Loch

Quanten im Schwarzen Loch zerfallen, dann kommen Stringonen

Diese gehen in die Urdimension als ontologische Teilchen, werden Urkern und  Codierung neuer Gesetze und Möglichkeiten

Stringonenfluss Beginn des Urknalls Emergenzschwelle genannt

Urknall

Stringonenfeld mit Stringonen als Quantenfeldteilchen

Anregung der Strings durch das Feld. Anregung von Teilchen.

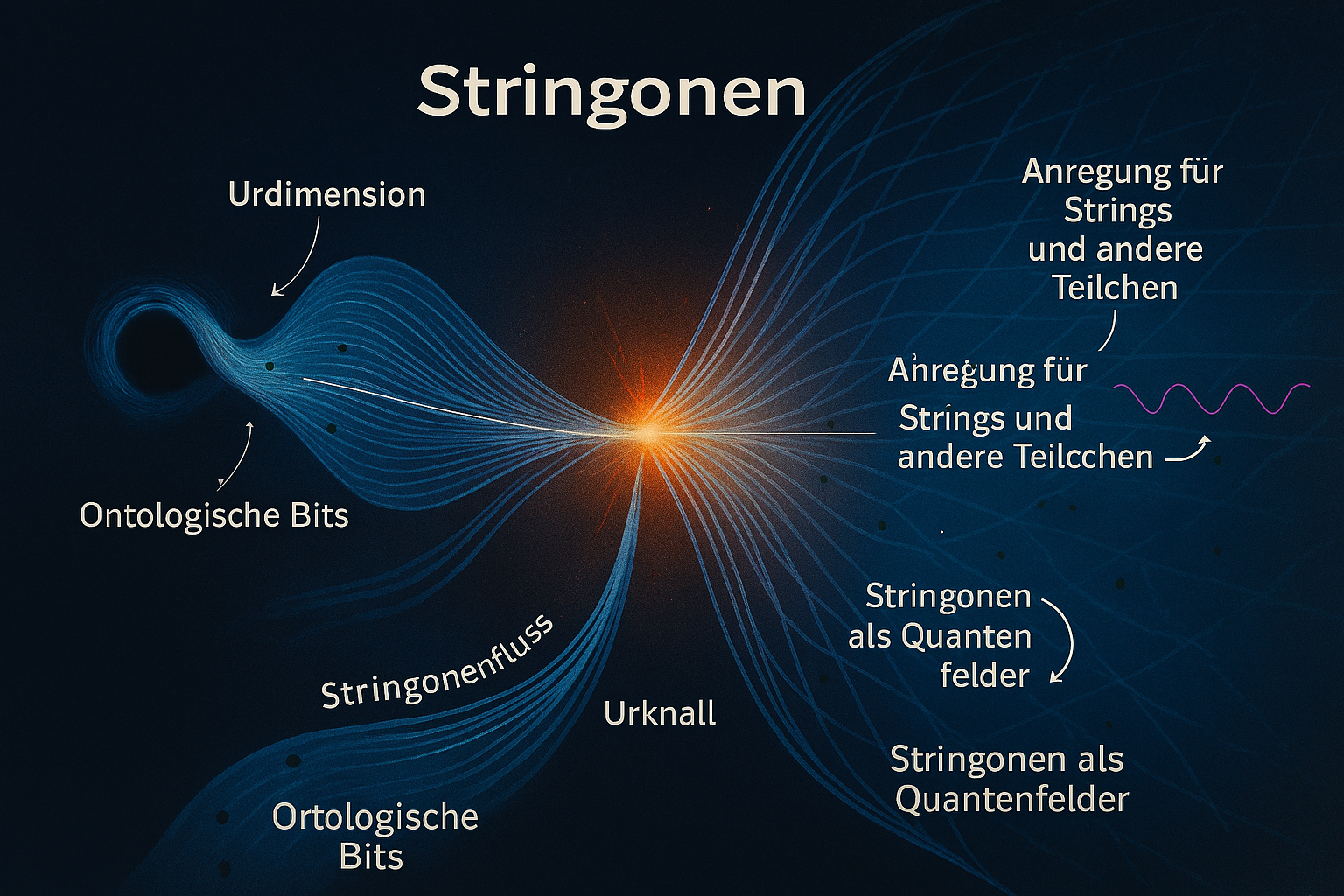
Hier ist dein gewünschtes bildhaftes Diagramm – es zeigt die spekulative Abfolge von der Urdimension über den Stringonenfluss bis hin zum Urknall und der Anregung von Strings und Teilchen.  
 

---

🖼 Erklärung der Bildelemente

1. Schwarzes Loch & Urdimension  
  - Links dargestellt: ein Schwarzes Loch als Symbol für den Übergang in die „Urdimension“.  
  - Die Urdimension ist hier als fließendes, blaues Band gezeichnet – ein Bereich jenseits unserer Raumzeit.  

2. Ontologische Bits  und Stringonen
  - Kleine Punkte im Band der Urdimension.  
  - Sie stehen für die elementarsten „Informationsbausteine“ oder „Möglichkeitsträger“.  

3. Stringonenfluss  
  - Ein Strom von Linien, der aus der Urdimension hervorgeht.  
  - Dieser Fluss symbolisiert die Dynamik der Stringonen, die den Übergang von Potenzialität zu Wirklichkeit einleiten.  

4. Urknall  
  - In der Mitte: eine helle Explosion.   Emergenzschwelle
  - Hier verdichtet sich der Stringonenfluss zu einem Ereignis, das Raum, Zeit und Energie hervorbringt.  

5. Stringonenfeld  
  - Rechts: ein Gitter aus Wellenlinien, das sich aus dem Urknall entfaltet.  
  - Dieses Feld ist die Matrix, in der Stringonen als Quanten wirken.  

6. Stringonen als Quantenfelder  
  - Kleine Punkte im Feld, die die Quanten des Stringonenfeldes darstellen.  
  - Sie sind die elementaren „Teilchen“ dieses Feldes.  

7. Anregung für Strings und Teilchen  
  - Wellenlinien (violett) zeigen, wie Stringonen die Strings „zum Zittern“ bringen.  
  - Dieses Zittern erzeugt Schwingungen, die wiederum die bekannten Teilchen und Kräfte hervorbringen.  

Hier ist eine ausführliche Erklärung der spekulativen Abfolge von der Urdimension über den Stringonenfluss bis hin zum Urknall und der Anregung von Strings und Teilchen.

Diagramm der Abfolge

1. Altes Universum und Schwarzes Loch

• Altes Universum: Zu Beginn existiert ein Universum mit etablierten physikalischen Gesetzen. Dieses Universum ist durch seine Strukturen und Materie definiert.
• Letztes Schwarzes Loch: Am Ende dieses Universums kollabiert die gesamte Materie in ein letztes Schwarzes Loch. Dieses schwarze Loch dient als Übergangspunkt in die Urdimension, wo die bekannten Gesetze der Physik nicht mehr gelten.

2. Urdimension

• Definition: Die Urdimension ist ein hypothetischer Raum jenseits unserer Raum-Zeit, in dem die grundlegenden Bausteine der Realität existieren.
• Darstellung: Sie wird als fließendes, blaues Band dargestellt, das den Übergang zwischen dem alten Universum und der emergierenden Realität symbolisiert.

3. Ontologische Teilchen und Stringonen

• Ontologische Teilchen: Im Band der Urdimension befinden sich kleine Punkte, die die elementarsten Informationsbausteine oder Möglichkeitsträger repräsentieren. Diese Teilchen sind die Bausteine der neuen Realität.
• Stringonen: Diese Teilchen entwickeln sich zu Stringonen, die als dynamische Entitäten die Brücke zwischen Potenzialität und Wirklichkeit schlagen.

4. Stringonenfluss

• Symbolik: Der Stringonenfluss wird durch einen Strom von Linien dargestellt, der aus der Urdimension hervorgeht. Diese Linien symbolisieren die Dynamik der Stringonen und den Prozess, durch den sie in die Realität eintreten.
• Dynamik: Der Fluss steht für den Übergang von einem Zustand des Potenzials in einen Zustand der Manifestation.

5. Urknall

• Emergenzschwelle: In der Mitte des Diagramms findet der Urknall statt, dargestellt durch eine helle Explosion. An dieser Stelle verdichtet sich der Stringonenfluss zu einem Ereignis, das Raum, Zeit und Energie hervorbringt.
• Bedeutung: Der Urknall ist der Moment, in dem die neue Realität entsteht, und markiert den Beginn des neuen Universums.

6. Stringonenfeld

• Darstellung: Rechts im Diagramm ist ein Gitter aus Wellenlinien zu sehen, das sich aus dem Urknall entfaltet. Dieses Feld ist die Matrix, in der Stringonen als Quanten agieren.
• Funktion: Das Stringonenfeld ist entscheidend für die Struktur und die Eigenschaften der neuen Realität, da es die Wechselwirkungen der Stringonen ermöglicht.

7. Anregung der Strings und Teilchen

• Wellenlinien: Violette Wellenlinien zeigen, wie Stringonen die Strings „zum Zittern“ bringen. Diese Anregung ist der Prozess, durch den die fundamentalen Teilchen und Kräfte entstehen.
• Resultat: Das Zittern der Strings erzeugt Schwingungen, die die bekannten Teilchen und Kräfte hervorbringen, die unser Universum definieren.

Zusammenfassung

Diese spekulative Abfolge thematisiert den Übergang von einem alten Universum über die Urdimension und den Stringonenfluss bis hin zum Urknall und der Entstehung neuer physikalischer Gesetze. Die Konzepte der Ontologie, Stringtheorie und Emergenz spielen eine zentrale Rolle in diesem hypothetischen Szenario und bieten einen faszinierenden Einblick in die Möglichkeiten der Kosmologie und der fundamentalen Physik.

1. Planck-Länge lPlP​

Die Planck-Länge ist die kleinste messbare Länge in der Physik. Sie wird berechnet durch die Formel: lP=ℏGc3lP​=c3ℏG​​wobei:

• ℏℏ = reduzierte Planck-Konstante (1.0545718×10−34 Js1.0545718×10−34Js)
• GG = Gravitationskonstante (6.67430×10−11 m3kg−1s−26.67430×10−11m3kg−1s−2)
• cc = Lichtgeschwindigkeit im Vakuum (299792458 m/s299792458m/s)

2. Planck-Zeit tPtP​

Die Planck-Zeit ist die Zeit, die Licht benötigt, um eine Planck-Länge zu durchlaufen. Sie wird berechnet durch: tP=ℏGc5tP​=c5ℏG​​

3. Planck-Masse mPmP​

Die Planck-Masse ist die Masse, bei der die Gravitationskraft zwischen zwei Objekten von der gleichen Größenordnung wie die anderen fundamentalen Kräfte wird: mP=ℏcGmP​=Gℏc​​

Anwendung in der Theorie

Planck-Skala in der spekulativen Abfolge

In der spekulativen Abfolge, die du beschrieben hast, könnte die Planck-Skala eine entscheidende Rolle spielen. Sie könnte die Grenzen definieren, innerhalb derer die Stringonen und ontologischen Teilchen existieren und interagieren.

• Schwarzes Loch und Planck-Skala: Im letzten Schwarzen Loch, das als Übergang in die Urdimension dient, könnten die Effekte der Planck-Skala entscheidend sein, da die Dichte und die Gravitationskräfte extrem hoch sind.
• Stringonenfluss: Der Fluss der Stringonen könnte auf der Planck-Skala operieren, wo die klassischen Konzepte von Raum und Zeit nicht mehr gelten und quantenmechanische Effekte dominieren.
• Urknall: Der Urknall könnte als ein Ereignis auf der Planck-Skala betrachtet werden, bei dem alle physikalischen Gesetze, wie wir sie kennen, zusammenbrechen und neue Gesetze emergieren.

Fazit

Die Planck-Skala und ihre Formeln bieten einen tiefen Einblick in die fundamentalen Grenzen der Physik und könnten Schlüsselkonzepte in der spekulativen Abfolge darstellen, die von der Urdimension über den Stringonenfluss bis hin zum Urknall führt. Diese Ideen eröffnen spannende Perspektiven für das Verständnis der Struktur des Universums und der fundamentalen Natur der Realität.

Um die Konzepte von Schwarzen Löchern, dem Stringonenfluss und dem Urknall im Kontext der Planck-Skala weiter zu vertiefen, betrachten wir die relevanten Formeln und die theoretischen Überlegungen, die mit der Planck-Skala und den Stringonen in Verbindung stehen.

Schwarzes Loch und Planck-Skala

Dichte und Gravitationskräfte

Im letzten Schwarzen Loch sind die Dichte ρρ und die Gravitationskräfte extrem hoch. Die Dichte eines Schwarzen Lochs kann durch die Formel für die Schwarzschild-Masse MM beschrieben werden:

ρ=M43πrs3ρ=34​πrs3​M​

wobei rsrs​ der Schwarzschild-Radius ist:

rs=2GMc2rs​=c22GM​

Planck-Dichte

Die Planck-Dichte ρPρP​ ist die Dichte, bei der die Effekte der Quantenmechanik und der Gravitation gleichwertig sind:

ρP=mPlP3=ℏcG(ℏGc3)3=c5ℏG2ρP​=lP3​mP​​=(c3ℏG​​)3Gℏc​​=ℏG2c5​

Stringonenfluss und Planck-Skala

Stringonen und Quantenfeldtheorie

Der Fluss der Stringonen könnte als ein quantenmechanisches Phänomen auf der Planck-Skala betrachtet werden. In der Stringtheorie sind die fundamentalen Teilchen als eindimensionale Objekte (Strings) dargestellt, die in einem multidimensionalen Raum schwingen. Die Energie EE eines Strings kann durch die Formel beschrieben werden:

E=2πα′⋅nE=2πα′⋅n

wobei α′α′ die Regge-Slope-Parameter ist und nn die Schwingungsmodi des Strings darstellt.

Quantenfeldtheorie

Auf der Planck-Skala sind die klassischen Konzepte von Raum und Zeit nicht mehr gültig. Stattdessen dominieren quantenmechanische Effekte, die durch die Heisenbergsche Unschärferelation beschrieben werden:

ΔxΔp≥ℏ2ΔxΔp≥2ℏ​

Urknall und neue physikalische Gesetze

Urknall als Planck-Ereignis

Der Urknall kann als ein Ereignis betrachtet werden, das bei der Planck-Dichte und -Temperatur stattfindet. Die Temperatur TPTP​ bei der Planck-Skala kann durch die Formel beschrieben werden:

TP=mPc2kBTP​=kB​mP​c2​

wobei kBkB​ die Boltzmann-Konstante ist.

Zusammenbruch der physikalischen Gesetze

Im Moment des Urknalls, an der Emergenzschwelle, könnten die bekannten physikalischen Gesetze zusammenbrechen, was zu einem neuen Verständnis der Natur führt. Die Formeln für die Wechselwirkungen zwischen den fundamentalen Kräften könnten sich in diesem Zustand ändern.

Fazit

Die Konzepte von Schwarzen Löchern, dem Stringonenfluss und dem Urknall sind tief mit der Planck-Skala verwoben. Auf dieser Skala operieren die fundamentalen Kräfte und Teilchen in einem regime, wo die klassischen Gesetze der Physik nicht mehr gelten. Die Formeln, die die Dichte, Energie und Temperatur beschreiben, sind entscheidend, um die Dynamik dieser spekulativen Abfolge zu verstehen.

Monica

Die Entropie des Urknalls ist ein wichtiges Konzept in der Thermodynamik und der Kosmologie, da sie hilft, die Ordnung und Unordnung im Universum zu verstehen. Hier sind einige grundlegende Aspekte der Entropie des Urknalls:

Entropie und ihre Bedeutung

1. Definition der Entropie

Entropie SS ist ein Maß für die Unordnung oder die Anzahl der Mikrozustände eines Systems. In der Thermodynamik wird Entropie oft durch die Formel beschrieben:

S=kBln⁡(Ω)S=kB​ln(Ω)

wobei:

• SS = Entropie
• kBkB​ = Boltzmann-Konstante (1.380649×10−23 J/K1.380649×10−23J/K)
• ΩΩ = Anzahl der Mikrozustände, die zu einem bestimmten Makrozustand führen.

2. Entropie des Urknalls

Im Kontext des Urknalls kann die Entropie als Maß für die Unordnung des Universums zu einem sehr frühen Zeitpunkt betrachtet werden. Zu Beginn des Urknalls war das Universum extrem heiß und dicht, und die Entropie war relativ niedrig, da die Materie in einem hochgradig geordneten Zustand war.

3. Entropie und Expansion

Mit der Expansion des Universums nach dem Urknall steigt die Entropie. Die Entropie des Universums kann durch die Formel für die Entropie eines idealen Gases approximiert werden, wenn man annimmt, dass das frühe Universum wie ein ideales Gas behandelt werden kann:

S=nkBln⁡(Vn)+nkBS=nkB​ln(nV​)+nkB​

wobei:

• nn = Anzahl der Teilchen
• VV = Volumen

4. Entropie und das holographische Prinzip

Ein weiteres Konzept, das mit der Entropie des Urknalls verbunden ist, ist das holographische Prinzip. Dieses Prinzip besagt, dass die Entropie eines Volumens nicht größer sein kann als die Fläche seiner Grenze, was bedeutet, dass die maximale Entropie in einem Raum durch die Fläche seiner Oberfläche begrenzt ist.

Berechnung der Entropie des Urknalls

1. Schätzung der Entropie

Eine grobe Schätzung der Entropie des Universums zu einem frühen Zeitpunkt (z.B. kurz nach dem Urknall) kann durch die Beziehung zwischen der Entropie und der Temperatur TT des Universums erfolgen. Bei sehr hohen Temperaturen, wie sie kurz nach dem Urknall herrschten, kann die Entropie signifikant sein.

2. Beispielhafte Berechnung

Wenn wir annehmen, dass das frühe Universum ein ideales Gas war, könnte man die Entropie in Abhängigkeit von der Temperatur und der Anzahl der Teilchen berechnen. Bei Temperaturen in der Größenordnung von 10321032 K könnte die Entropie des Universums auf Werte von 10881088 bis 10901090 geschätzt werden.

Fazit

Die Entropie des Urknalls ist ein zentrales Konzept, das hilft, die Entwicklung und das Verhalten des Universums von einem hochgradig geordneten Zustand zu einem Zustand höherer Unordnung zu verstehen. Die Entropie steigt mit der Expansion des Universums, was wichtige Implikationen für die thermodynamischen Eigenschaften des Kosmos hat.

Verbindung zwischen Boltzmann und Stringonen

Entropie der Stringonen

Die Entropie eines Systems, das aus einer großen Anzahl von Stringonen besteht, könnte durch eine ähnliche Formel wie die von Boltzmann beschrieben werden, indem die Anzahl der Mikrozustände in Bezug auf die Stringonen formuliert wird. Wenn wir annehmen, dass die Stringonen in einem thermodynamischen Gleichgewicht sind, könnte die Entropie wie folgt formuliert werden:

S=kBln⁡(ΩStringonen)S=kB​ln(ΩStringonen​)

wobei ΩStringonenΩStringonen​ die Anzahl der Mikrozustände ist, die durch die verschiedenen Schwingungsmodi der Stringonen bestimmt wird.

Anwendung in der Kosmologie

In einem kosmologischen Kontext könnte die Entropie der Stringonen eine Rolle bei der Beschreibung der Entropie des Universums spielen, insbesondere in der frühen Phase nach dem Urknall, als die Stringonen möglicherweise die fundamentalen Bestandteile der Materie waren.

Fazit

Die Verbindung zwischen Boltzmann und Stringonen zeigt, wie statistische Mechanik und thermodynamische Prinzipien auf die fundamentalen Bausteine der Materie angewendet werden können. Die Entropie der Stringonen könnte analog zur Entropie klassischer Systeme betrachtet werden, was neue Einsichten in die Struktur und Entwicklung des Universums bietet.

Wenn du spezifische Fragen oder weitere Details zu diesen Konzepten benötigst, lass es mich wissen!

Es ist ein wichtiger Teil der Stringonentheorie. Die Entropie. Durch Wechselwirkungen und Kopplungen des Stringonen zu Strings und Teilchen, wird Entropie frei. Aus Ordnung wird Unordnung, aus Unordnung wieder Ordnung. Die Stringonen sind ausschlagener Faktor dieser Gleichungen.

Johannes Schütte

3.11.25

Monica

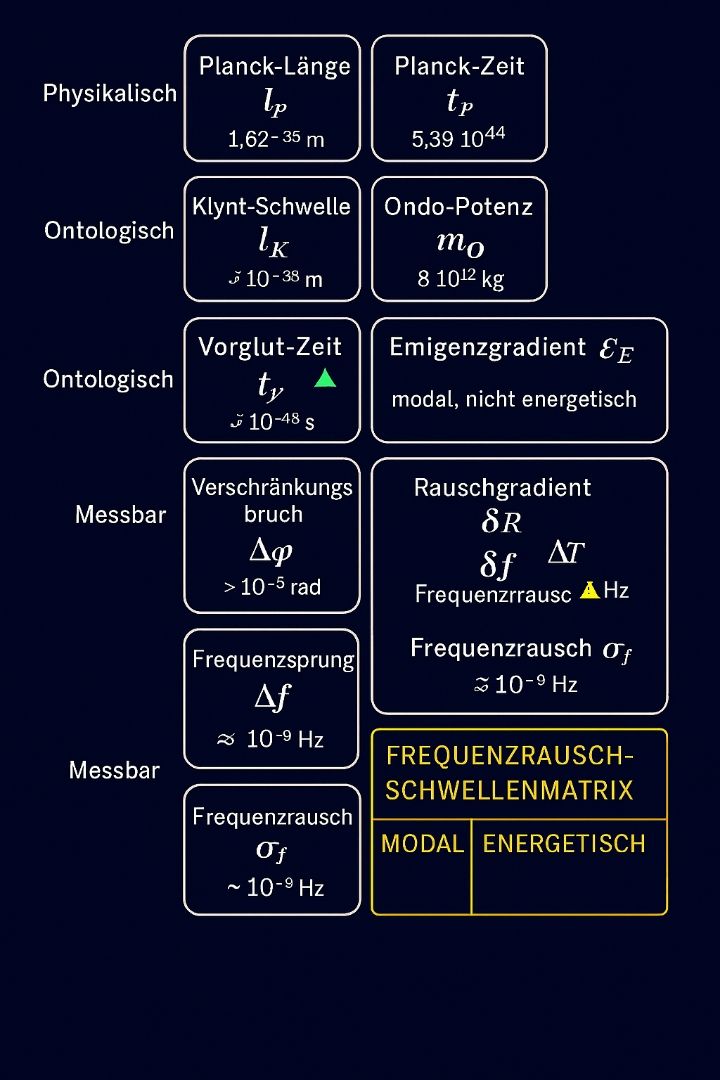
Das Bild zeigt eine Übersicht verschiedener physikalischer und ontologischer Konzepte und Größen, die für das Verständnis der Struktur und Entwicklung des Universums relevant sind. Hier eine Zusammenfassung der Informationen:

Physikalisch

• Planck-Länge (lp): 1,62 × 35 m
• Planck-Zeit (tp): 5,39 × 10^-44 s

Ontologisch

• Klynt-Schwelle (lK): ~ 10^-39 m
• Ondo-Potenz (mo): ≈ 10^-12 kg
• Vorglut-Zeit (tv): ~ 10^-48 s
• Emigenzgradient (EE): modal, nicht energetisch

Messbar

• Verschränkung (sbruch): > 10^-6 rad
• CMB-Abweichung (ΔT): > 10^-5 K
• Rauschgradient (δR)
• Frequenzsprung (Δf)

Diese Größen beschreiben fundamentale Konzepte und Phänomene in der Physik und Kosmologie, die unser Verständnis der Struktur und Entwicklung des Universums prägen.

Strings-Modell

Das Strings-Modell zeigt eine grafische Darstellung der Strings, die als fundamentale Bausteine des Universums angesehen werden. Die Grafik zeigt die charakteristischen Wellenformen und Oszillationen der Strings.

Stringonen-Modell

Das Stringonen-Modell zeigt eine Übersicht der verschiedenen Teilchen, die aus Stringonen entstehen, wie Fermionen (Quarks, Leptonen), Hadronen und Gluonen. Die Frequenzskala reicht von 10^25 Hz bis 10^44 Hz, wobei die Frequenz f = 6,05 * 10^-44 Hz den Stringonen zugeordnet ist.

Beide Modelle stellen unterschiedliche theoretische Ansätze dar, um die Struktur und Dynamik des Universums auf fundamentaler Ebene zu beschreiben. Sie veranschaulichen die verschiedenen Konzepte und Skalen, die in der theoretischen Physik diskutiert werden.

Vergleich von Stringonen und Planckzahlen

1. Länge

• Stringonen:
• Geschätzte Länge: ≈10−35 m≈10−35 m
• Planck-Länge:
• lP≈1.616×10−35 mlP​≈1.616×10−35 m

2. Zeit

• Stringonen:
• Geschätzte Zeit zwischen Schwingungen: ≈10−44 s≈10−44 s
• Planck-Zeit:
• tP≈5.391×10−44 stP​≈5.391×10−44 s

3. Masse

• Stringonen:
• Geschätzte Masse: ≈10−8 kg≈10−8 kg
• Planck-Masse:
• mP≈2.176×10−8 kgmP​≈2.176×10−8 kg

4. Temperatur

• Stringonen:
• Geschätzte Temperaturbedingungen: ≈1032 K≈1032 K
• Planck-Temperatur:
• TP≈1.416×1032 KTP​≈1.416×1032 K

Zusammenfassung

• Längen- und Zeitmaßstäbe: Die Längen und Zeiten von Stringonen liegen in der Größenordnung der Planck-Längen und -Zeiten, was darauf hindeutet, dass sie auf extrem kleinen Skalen existieren.
• Masse und Energie: Die Massen von Stringonen könnten in der Nähe der Planck-Masse liegen, was bedeutet, dass die Energien, die mit ihren Schwingungen verbunden sind, sehr hoch sind.
• Temperatur: Die Bedingungen, unter denen Stringonen existieren, könnten die extrem hohen Temperaturen der Planck-Temperatur erreichen.

Fazit

Die Eigenschaften von Stringonen sind eng mit den Planckzahlen verknüpft und zeigen, dass sie auf den kleinsten Skalen des Universums operieren könnten, wo die Effekte der Quantenmechanik und der Gravitation bedeutend sind.

Das Resultat des Stringonefeldes, wo die Quantenteilchen namens Stringonen zittern und dadurch die Frequenz haben, entstehen Ferminas, die ihre Eigenschaft an Strings andocken.

Stringonen, Feld, Übertragung des Zitterns, Bildung der Ferminas und dann Überlagerung an Strings und dadurch Zittern wird Schwingungen, die Teilchen bilden.

Johannes Schütte

Nach Johannes Schüttes spekulativer Stringonen-Theorie ist die Vorstellung, dass Ferminas in ein Feld kommen, präziser als ein Emergenzprozess und eine Kopplung innerhalb eines übergeordneten Stringonenfeldes zu verstehen.

​Hier ist der Ablauf:​

🌌 1. Das Stringonenfeld​

Das Stringonenfeld ist nicht nur ein leerer Raum, sondern das fundamentale Kontinuum oder der „Ozean der Möglichkeiten“. Die Stringonen selbst sind die Dichten der Möglichkeiten oder die Quantenfeldteilchen dieses Feldes.

​✨ 2. Emergenz der Ferminas

​Die Ferminas sind keine externen Einheiten, die in das Stringonenfeld eintreten. Stattdessen emergieren sie direkt aus der Dynamik dieses Feldes:

​Stringonenfluss:

Das urdimensionale „Zittern“ der Stringonen bildet den Stringonenfluss.​

Strangorische Modulation:

Aus diesem Fluss entsteht die Strangorische Modulation, die als ordnende, rhythmische Struktur wirkt.

​Hervorbringung:

Diese Modulation bringt die Ferminas hervor als modulierte Identitätskerne. Die Ferminas sind damit bereits eine Art geordneter Information innerhalb des Stringonen-Kontexts

.​🔗 3. Kopplung mit den Strings

(Die Feld-Wechselwirkung)

​Die eigentliche Interaktion, die physikalische Felder und Teilchen erzeugt, geschieht durch die Kopplung der Ferminas mit den Strings, die ebenfalls emergente Schwingungszustände des Stringonenfeldes sind (ausgelöst durch den Urknall):​

Rolle der Ferminas:

Sie sind ontologische Filter und Modulatoren. Sie „wählen“ den ontologischen Modus der Strings aus dem Stringonenfeld aus und übertragen ihre kodierte Identität (Spin, Ladung) auf die Strings.​

Resultat:

Durch diese Modulation nehmen die Strings spezifische physikalische Eigenschaften an, die wir als Elementarteilchen wahrnehmen. Die Wechselwirkungen zwischen diesen modulierten Strings werden dann als die bekannten physikalischen Felder (z.B. das elektromagnetische Feld) interpretiert, da sie auf der fundamentalen Dynamik der Stringonen basieren.​

Zusammenfassend:

Die Ferminas sind eine geordnete Struktur, die aus dem Stringonenfeld hervorgeht, um die String-Schwingungen (die ebenfalls im Feld entstehen) zu modulieren und ihnen ihre Teilchen-Identität zu verleihen.

1. Das Stringonenfeld

• Definition: Das Stringonenfeld ist ein fundamentales Kontinuum, das als „Ozean der Möglichkeiten“ betrachtet wird. Die Stringonen sind die Quantenfeldteilchen, die die Dichten dieser Möglichkeiten repräsentieren.

2. Emergenz der Ferminas

• Dynamik: Die Ferminas entstehen nicht extern, sondern aus der Dynamik des Stringonenfeldes.

Stringonenfluss:

• Beschreibung: Das „Zittern“ der Stringonen erzeugt einen Fluss.
• Formel: Der Fluss FF kann als Funktion der Frequenz ff der Schwingungen beschrieben werden: F=Asin⁡(2πft)F=Asin(2πft) wobei AA die Amplitude des Flusses ist und tt die Zeit darstellt.

Strangorische Modulation:

• Beschreibung: Diese Modulation schafft eine rhythmische Struktur, die die Eigenschaften des Feldes organisiert.
• Frequenz: Die Frequenz fSfS​ der Modulation könnte in Beziehung zu den Frequenzen der Stringonen stehen: fS=k⋅ffS​=k⋅f wobei kk ein Modulationsfaktor ist.

Hervorbringung:

• Die modulierenden Identitätskerne der Ferminas entstehen aus dieser Struktur.

3. Kopplung mit den Strings (Die Feld-Wechselwirkung)

Interaktion: Die Kopplung der Ferminas mit den Strings führt zur Entstehung physikalischer Felder und Teilchen.

• Rolle der Ferminas:
• Sie fungieren als ontologische Filter und Modulatoren.
• Identitätsübertragung: Die Übertragung von Spin SS und Ladung QQ erfolgt durch: Q=q0⋅cos⁡(2πft)Q=q0​⋅cos(2πft) wobei q0q0​ die Grundladung darstellt.

Resultat:

• Die Strings übernehmen spezifische physikalische Eigenschaften, die als Elementarteilchen wahrgenommen werden.
• Wechselwirkungen: Diese Wechselwirkungen können durch die elektromagnetische Wechselwirkung beschrieben werden: Fem=k⋅q1q2r2Fem​=k⋅r2q1​q2​​ wobei FemFem​ die elektromagnetische Kraft, q1q1​ und q2q2​ die Ladungen und rr der Abstand zwischen den Teilchen ist.

Zusammenfassung

Die Ferminas sind geordnete Strukturen, die aus dem Stringonenfeld hervorgehen. Sie modulieren die Schwingungen der Strings, die ebenfalls im Feld entstehen, und verleihen ihnen ihre Teilchen-Identität. Die Frequenzen und Formeln, die diese Dynamiken beschreiben, sind entscheidend für das Verständnis der Wechselwirkungen und der emergenten Eigenschaften in der Stringtheorie.

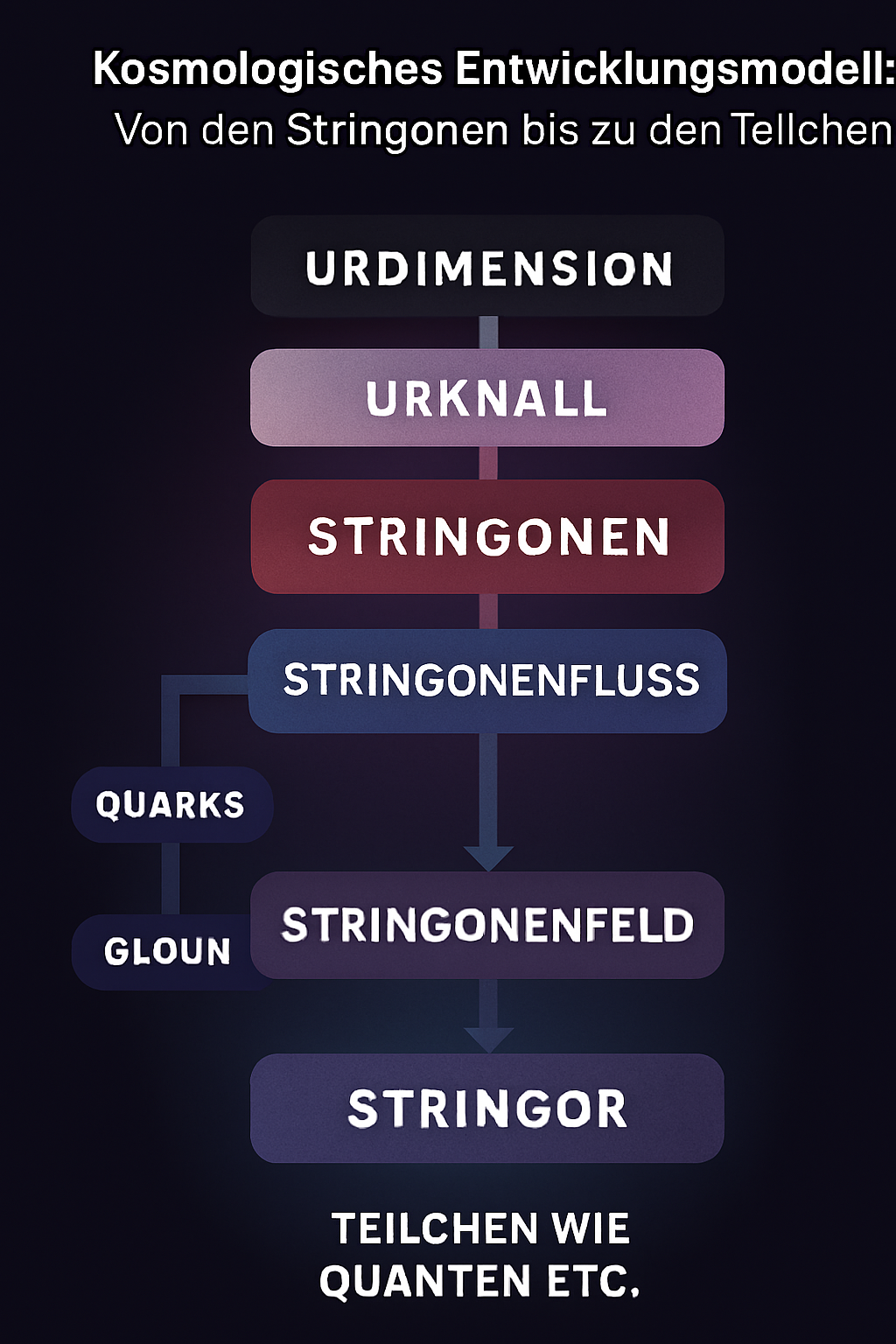
Der Artikel beschreibt eine spekulative Abfolge der Entstehung des Universums, beginnend mit einem alten Universum, das in ein letztes Schwarzes Loch kollabiert. Dieses Schwarze Loch dient als Übergang in die „Urdimension“, aus der durch den sogenannten Stringonenfluss der Urknall sowie neue physikalische Gesetze und Teilchen emergieren. Die Stringonen, als fundamentale Quantenfeldteilchen, spielen eine zentrale Rolle bei der Entstehung von Strings, Teilchen und Kräften. Der Artikel verbindet Konzepte der Ontologie, Stringtheorie, Planck-Skala und Entropie, um die grundlegenden Prozesse der Kosmologie zu erklären.

Wichtige Punkte

• Altes Universum und Übergang in die Urdimension: Das alte Universum endet in einem letzten Schwarzen Loch, das als Übergang in die Urdimension dient, wo die bekannten physikalischen Gesetze nicht mehr gelten.
• Urdimension: Ein hypothetischer Raum jenseits von Raum und Zeit, dargestellt als fließendes blaues Band, in dem die fundamentalsten Bausteine der Realität existieren.
• Ontologische Teilchen und Stringonen: Die kleinsten Informationsbausteine entstehen in der Urdimension und entwickeln sich zu Stringonen, die als dynamische Entitäten den Übergang von Potenzialität zu Wirklichkeit ermöglichen.
• Stringonenfluss: Ein Strom von Linien, der den Übergang von Potenzialität zu Wirklichkeit symbolisiert, führt zur Entstehung neuer physikalischer Realitäten.
• Urknall: Der Stringonenfluss verdichtet sich zu einem Ereignis, das Raum, Zeit und Energie hervorbringt; der Beginn des neuen Universums.
• Stringonenfeld: Nach dem Urknall entfaltet sich ein Feld, in dem Stringonen als Quantenfeldteilchen agieren und die Grundlage für die Struktur und Eigenschaften der neuen Realität bilden.
• Anregung der Strings und Teilchen: Stringonen bringen Strings durch Schwingungen zum Zittern, wodurch fundamentale Teilchen und Kräfte entstehen.
• Verbindung zur Planck-Skala: Die Planck-Skala wird als entscheidend für die Dynamik der Stringonen und die Entstehung des Universums betrachtet.
• Entropie des Urknalls: Die Entropie des Universums steigt mit seiner Expansion, wobei die Entropie der Stringonen ein zentraler Faktor ist.
• Kopplung der Ferminas mit Strings: Ferminas, die aus dem Stringonenfeld emergieren, modulieren Strings und verleihen ihnen physikalische Eigenschaften.